El pensament més sortat d’Albert Einstein

Que Albert Einstein fou un gran geni ningú ho posa en dubte. Quan tenia 25 anys va redactar quatre treballs tan importants que cadascun d’ells podria haver-li fet merèixer un premi Nobel. I això que encara no se li havia acudit la idea més genial de totes! Ell mateix confessà que quan la va tenir, aquell dia de novembre del 1907, experimentà de sobte un gran calfred que li va recórrer el cos i el deixà clavat a la cadira, estupefacte. En veurem els detalls tot seguit.

Quan va començar el segle XXI, la prestigiosa revista Time va haver d’escollir, per a la portada, el personatge més important de tot el segle XX. L’elegit va ser justament Albert Einstein. La seva icònica imatge aparegué al número corresponent al 31 de desembre de 1999. Aquesta important decisió fou justificada amb afirmacions com ara:

“D’aquí a cent anys, d’aquí a cent vegades cent anys, per molts mil·lennis que passin, el nom més perdurable de la nostra era continuarà sent sense cap dubte el d’Albert Einstein.”

Això ens fa recordar també el que el gran matemàtic Godfrey Hardy, descobridor d’un altre geni, Srinivasa Ramanujan, va escriure una vegada:

“Les matemàtiques gregues són permanents, molt més encara que l’excelsa literatura grega. Els idiomes moren, en canvi, les idees matemàtiques sobreviuen per sempre.”

La idea se li va ocórrer l’any 1907

Dit això, esdevé més important encara conèixer de primera mà quina va ser la idea més brillant que Einstein va tenir en tota la seva vida. Doncs és ben curiós que fos ell mateix qui ho va explicar, al menys en dues ocasions, sense necessitat que ningú li ho preguntés. El genial pensament li va venir el 1907, mentre treballava a l’Oficina Suïssa de Patents, a Berna (Fig. 1).

Fig 1. Albert Einstein a l’Oficina Suïssa de Patents - Crèdit: ETH-Bibliothek Zürich, Bildarchiv. Domini públic.

Després de graduar-se, l’any 1900, pel Politècnic de Zúric, durant algun temps no fou capaç de trobar feina a la universitat (aquest fet hauria de servir d’estímul als joves prometedors que es puguin trobar ara en les mateixes circumstàncies). Es va haver de conformar amb treballar com a tutor a Winterthur, Schaffhausen i Berna. El seu company de classe Marcel Grossmann —que més tard li donaria un cop de mà en la formulació matemàtica de la relativitat general— fou precisament qui va fer de mitjancer perquè el contractessin a l’esmentada Oficina de Patents de Berna. Einstein parlava poc i no es pot dir que donés gaire bona imatge. Aquesta va ser la seva principal ocupació des del juny de 1902 fins a l'octubre de 1909. I fou allí precisament on, a estones perdudes, entre patent i patent, van sorgir de la seva ment els quatre treballs tan brillants ja esmentats, i encara un cinquè, que foren publicats el 1905. Aquell any se’l coneix avui com l’annus mirabilis d’Einstein, i per celebrar-ne el centenari, el 2005 fou declarat a nivell mundial l’Any de la Física.

Però tornem al 1907 [1]. Com qualsevol altre dia, Einstein estava assegut a la seva cadira habitual, davant la seva taula de treball, quan, de sobte, es va sobresaltar molt al passar-li pel cap el que més tard qualificaria com a “pensament més afortunat de la meva vida” (“ich kam auf den glücklichsten Gedanken meines Lebens”). Tot de cop, va imaginar-se què succeiria si en aquell precís instant estigués caiguent en posició vertical des de la teulada de casa seva. Raonà que, mentre caigués, no estaria pas sotmès a cap camp gravitatori: cauria lliurement com si la gravetat al seu entorn no existís. Si, en aquell instant, sostingués un objecte sobre el palmell de la mà (una moneda, una poma) i el deixés caure tombant la mà, l’objecte no cauria als seus peus! La poma seguiria al costat de la mà sense allunyar-se’n. No experimentaria cap gravetat! (Fig. 2).

Fig. 2. La idea més genial d’Albert Einstein. Si, mentre caigués de la teulada, sostingués un objecte sobre el palmell de la mà (una moneda, una poma) i el deixés caure tombant la mà, l’objecte no cauria pas als seus peus! La poma seguiria sempre al costat de la mà - Imatges creades per l’autor amb l’ajut de programes d’IA.

Amb altres paraules, i usant un llenguatge més tècnic, en deixar-se caure, Einstein s’hauria situat en un sistema accelerat (amb la mateixa acceleració que la gravetat produeix) i hauria eliminat d’aquesta manera la força gravitatòria al seu entorn: els objectes que tenia amb ell ja no caurien als seus peus! Tal com va confessar més tard, aquell va ser el dia en què es gestà en el seu cervell la teoria general de la relativitat (TGR).

Segons com es miri, aquesta gran idea ens pot semblar del tot banal, digna del mateix Perogrullo. Però, cal reflexionar-hi una mica, perquè és de pensades aparentment trivials d’on sorgeixen les teories més extraordinàries, que una vegada formulades i elaborades, ens resulten a vegades inabastables.

Una cosa molt semblant li havia passat a Newton

Talment havia passat ja, segles enrere, amb el descobriment d’Isaac Newton de la llei de gravitació universal. Diuen que un dia, mentre descansava al jardí, va fixar l’atenció en una poma [2] mentre aquesta queia sobre l’herba (Fig. 3). De sobte, es va adonar que la força amb què la Terra atreia la poma devia ser la mateixa amb què atrapava la Lluna, obligant-la a fer voltes i voltes. I el mateix deuria passar amb el Sol i els seus planetes; i amb tots els altres objectes del cel.

Fig. 3. Caricatura de la famosa història sobre com Isaac Newton podria haver descobert la llei de la gravitació; fixant-se en una poma que cau de l’arbre mentre contempla alhora la Lluna i s’adona que tots els objectes (terrestres i celestes) estan sotmesos a una mateixa força: la gravetat. Imatge: Alexander Borek, creada: 23 setembre 2019, CC-BY-SA-4.0

D’acord amb l’aclamada llei de la gravitació universal —formulada per Newton després de fer-ne les comprovacions pertinents— tots els objectes de l’Univers s’atreuen entre ells, amb una força proporcional al producte de les seves masses respectives i inversament proporcional al quadrat de la distància que els separa. Llei extraordinària, inigualable, i que semblava definitiva.

Però no va ser-ho, finalment: ni universal ni definitiva. Amb la seva idea genial, Einstein fou capaç d’anar molt més enllà, emulant els arriscats mariners que van trobar un nou món. En imaginar-se caient des de la teulada de casa seva, va descobrir que podia eliminar completament la força de la gravetat: la poma que Einstein duria al palmell de la mà ja no li cauria ara als peus, sinó que, quan la deixés anar romandria sempre al costat de la mà. Va saber de seguida que havia descobert una cosa d’extraordinària importància.

Fig. 4. Einstein en caiguda lliure - Imatge creada a través de Difusió Estable. Domini públic. https://stablediffusionweb.com/es#faq

El va anomenar principi d’equivalència

I va ser així. Demostrà amb aquesta pensada que les masses i el camp gravitatori poden fer-se desaparèixer, sent substituïts per un simple moviment accelerat, és a dir (en termes matemàtics) per la geometria, per la curvatura de l’espai-temps (Fig. 4). La teoria de la gravetat d’Einstein és, tota ella de fet, una teoria de l’espai i el temps. Aquest va ser sens dubte el seu descobriment més extraordinari. És cert que encara li va costar una desena d’anys arribar a obtenir les equacions de la seva teoria general de la relativitat, que són, de fet, les úniques fórmules capaces d’expressar matemàticament la genial idea que havia tingut en aquell precís instant i que anomenà el principi d’equivalència.

Amb les seves pròpies paraules, pronunciades en una conferència que va impartir el 1922 a la Universitat de Kyoto, durant el seu famós viatge per l’Orient Llunyà, Palestina i Espanya (podeu llegir el meu article “Contextos històric i científic entorn de la visita d’Einstein a Catalunya”):

“... quan una persona es troba en caiguda lliure, no sent el seu propi pes. Em vaig quedar molt sorprès. Aquest senzill pensament va causar una profunda impressió en mi. Em va portar fins a una nova teoria de la gravitació”.

La idea que va tenir a l’Oficina de Patents aquell dia de novembre de 1907 fou sens dubte “la més sortada” de la seva vida. Així ho havia afirmat ja abans, l’any 1920, en una ressenya que va escriure per a la revista Nature però que al final no fou publicada, perquè els editors van considerar que era massa llarga per encabir-la a la revista [3].

A la bibliografia ha estat més utilitzat l’exemple d’un ascensor en caiguda lliure, amb una persona a dins, com a alternativa per il·lustrar el mateix concepte. I una altra descripció, més actual i completament anàloga, és la que vaig explicar a “El principi d’equivalència relativista per a escèptics i descreguts” i que resumeixo tot seguit. Tanquem un observador en una càpsula situada a l’espai exterior, sense gravetat, i (1) dipositem la càpsula sobre un planeta, o alternativament, (2) sotmetem la càpsula a una força del mateix valor que la gravetat del planeta, realitzada amb un propulsor que empeny la càpsula cap amunt, imitant-ne amb precisió la gravetat. Per a l’observador dins de la càpsula, la situació (1) serà completament indistingible de la (2): mai no podrà esbrinar si és la gravetat o una força mecànica equivalent la que l’atreu cap a terra i li permet jugar normalment amb la pilota (Fig. 5).

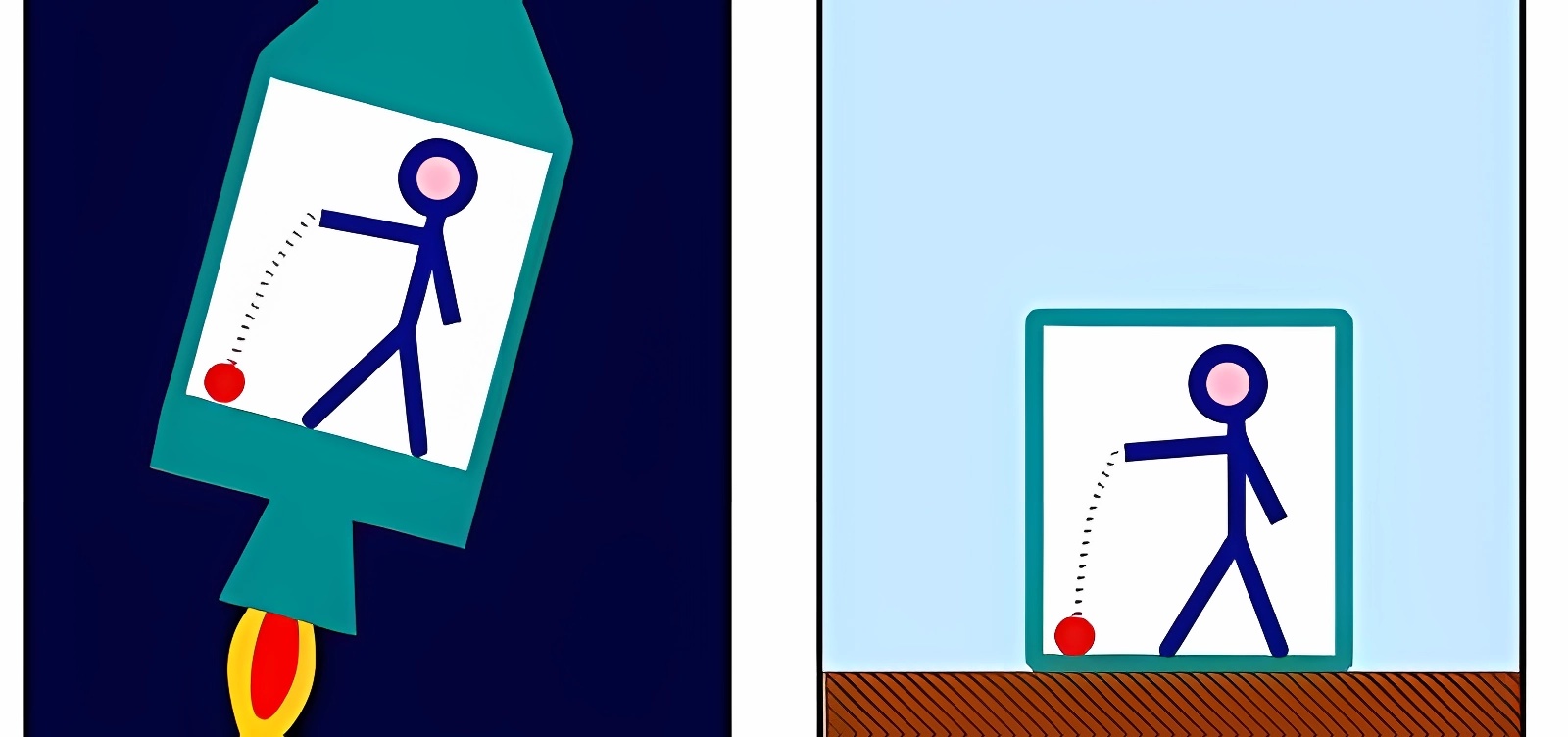
Fig. 5. L’observador dins de la càpsula no pot distingir si és la gravetat (dreta) o, en ingravidesa, una força mecànica de la mateixa magnitud realitzada per un propulsor (esquerra) allò que l’atreu cap avall i li permet jugar normalment amb la pilota - Imatge: Mapos, versió vectorial Perhelio. Ús raonable.

En conclusió, la gravetat pot ser substituïda per una força mecànica equivalent. No té res d’especial com a força. Això és precisament el que estableix el principi d’equivalència d’Einstein, pilar fonamental de la seva TGR. Teoria que descriu el nostre Univers amb una precisió extraordinària, i que ha estat confirmada en moltíssimes observacions i experiments.

Resumint: (a) La gravetat no és una força en el sentit clàssic, sinó que és una manifestació de la curvatura de l’espai-temps causada per la presència de masses i energies a l’Univers. (b) Malgrat tractar-se d’una força de naturalesa tan diferent, és del tot equivalent a qualsevol altra força: la massa gravitatòria d’un cos —la que intervé en la fórmula de Newton de l’atracció gravitatòria— és exactament la mateixa que la que oposa el cos a ser accelerat quan se li aplica qualsevol altra força (massa inert). Vet aquí una altra formulació del principi d’equivalència.

Com a colofó, el mateix Stephen Hawking —que va fer el meravellós descobriment que un forat negre irradia segons una llei perfecta de cos negre i a una temperatura que involucra les més belles constants fonamentals de la naturalesa— va voler experimentar, abans de morir, el que Einstein havia dit. I va verificar en persona, el 26 d’abril de 2016, dins d’un avió en caiguda lliure, en el seu cos malmès —alliberat finalment com les errants estrelles— que el principi d’equivalència de la relativitat general era correcte: la gravetat no és res més que una propietat emergent de l’espai-temps, del sistema de referència de l’Univers.

Nombroses aplicacions pràctiques molt importants

El principi d’equivalència té avui dia nombroses i molt importants aplicacions pràctiques, com ara en les correccions, que resulten del tot imprescindibles, al sistema de posicionament global (GPS), en el mesurament ultraprecís del temps, en geodèsia i per detectar variacions gravitacionals a la Terra, tan necessàries en diversos experiments (com per estudiar canvis en el nivell del mar, foses de glaceres, i variacions en aigües subterrànies), en l’estudi de forats negres i la detecció d’ones gravitacionals, o en els sistemes de navegació inercial dels submarins i avions que no fan servir el GPS, per parlar tan sols d’un grapat d’exemples.

Ja per acabar, i en un to més festiu, esmentaré l’efecte de la gravetat sobre el temps, que és conseqüència de la teoria. El podem presentar breument, com se sol fer, afirmant que el nostre veí de l’àtic envelleix més de pressa que la nostra veïna del pis principal, i aquesta més que el porter del bloc (si és que encara n’hi ha). Tot i que, de fet, només es guanyen uns 10^-6 segons en tota una vida, per cada metre de diferència en altura. Som doncs un xic afortunats —ja que viurem una miqueta més— si tenim l’apartament al segon pis i no pas al cinquè.

Referències

1. A. Einstein, “Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen”, Jahrbuch der Radioaktivität und Elektronik, 4, 411-462, 1907.
2. J.M. Montejo Bernardo, “¿De verdad recibió Newton un manzanazo?”, The Conversation, 27 gener 2019.
3. A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein, Oxford University Press, 1982.
4. E. Elizalde, “La esencia de la teoría de la relatividad de Einstein”, The Conversation, 9 gener 2024.

NOTA:

Aquest article és una traducció lliure al català de l’article que l’autor va publicar a la revista Muy Interesante amb el títol: “Esta es la idea más brillante de Albert Einstein que cambió para siempre nuestra comprensión de la gravedad y el espacio-tiempo”