Nombres perfectes, abundants i deficients

Un nombre perfecte és aquell que és igual a la suma dels seus divisors, exceptuant ell mateix (anomenats divisors propis). Per exemple, els divisors de 6 —llevat ell mateix— són 1, 2, 3, la suma dels quals és 6 (1+2+3=6). Per tant, el 6 és perfecte.

Els quatre primers nombres perfectes són 6, 28, 496 i 8.128, i fins ara, només es coneixen 51 nombres perfectes.

6 = 1+2+3

28 = 1+2+4+7+14

496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

8.128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1.016 + 2.032 + 4.064

Com a curiositats relacionades amb aquests nombres, i més enllà de les matemàtiques, us diré que sant Agustí d’Hipona (354-430), en el seu llibre La ciutat de Déu, ja comentava que Déu va crear el món en sis dies i que per això el nombre 6 és perfecte. Anàlogament, també es determina perfecte el nombre 28, perquè 28 són els dies que triga la Lluna a fer una volta al voltant de la Terra. I finalment, el nombre perfecte 8.128 va ser un dels premiats a la loteria de Nadal de l’any 2011.

Tornant a les matemàtiques, Euclides va demostrar que si un nombre de la forma M_n=2ⁿ-1 és primer, aleshores 2^n-1·M_n=2^n-1·(2ⁿ-1) és un nombre perfecte. Aquest fet també el va fer notar el científic francès Marin Mersenne (1588-1648), i per això els nombres de la forma M_n=2ⁿ-1 que són primers es diuen primers de Mersenne.

Si ens fixem en els quatre primers nombres perfectes veiem que s’obtenen dels quatre primers nombres primers de Mersenne:

per a n = 2:  2¹(2² − 1) = 6

per a n = 3:  2²(2³ − 1) = 28

per a n = 5:  2⁴(2⁵ − 1) = 496

per a n = 7:  2⁶(2⁷ − 1) = 8.128

Aquests primers quatre nombres perfectes ja apareixen en el document Introducció a l’aritmètica, de Nicòmac de Gerasa (segle I), un tractat de teoria de nombres —referent en la recerca en teoria de nombres durant més de 10 segles— que presenta les propietats dels nombres primers i dels nombres perfectes.

El cinquè nombre perfecte és el 33.550.336 (que correspon a n=13), i apareix documentat en un manuscrit del segle XV. El sisè (per a n=17) és 8.589.869.056 i el setè (per a n=19) és 137.438.691.328, i van ser descoberts per Pietro Cataldi l’any 1588. El vuitè el va descobrir Leonhard Euler el 1772 per a n=31, i el seu valor és:

 2³⁰ (2³¹ – 1) = 2.305.843.008.139.952.128

Aquest matemàtic suís va demostrar també que tots els nombres perfectes parells són d’aquesta forma. Finalment, cal dir que el 7 de desembre de 2018 es va trobar el major nombre perfecte conegut:

2^82589932·(2^82589933-1)

Tot plegat ens dona una idea que per generar nombres perfectes a partir d’un nombre primer de Mersenne, del tipus (2ⁿ-1), n’hi ha prou amb multiplicar aquest nombre per 2ⁿ-1. Tots els nombres perfectes generats d’aquesta manera són parells i acaben en 6 o 8, i no s’ha pogut demostrar l’existència de nombres perfectes senars.

Aquesta regla es coneix com a teorema d’Euclides-Euler dels nombres perfectes i es va publicar el 1849 en l’obra pòstuma d’Euler Tratactus de numerorum doctrina que posteriorment completa en De numeris amicabilibus.

Aprofitant que he parlat del tractat de Nicòmac, us vull recordar que en aquest llibre es va definir també el concepte de nombre abundant i el designa com a aquell nombre natural que és menor que la suma dels seus divisors propis. Els primers nombres abundants són el 12, 18, 24, 30, etc. En el cas del 12 són divisors propis 1, 2, 3, 4 i 6, i si sumem 1+2+3+4+6 = 16, el resultat confirma que efectivament 12 és més petit que 16. 

Dels nombres abundants, podem dir que el primer nombre abundant imparell és el 945, mentre que s’ha demostrat que qualsevol nombre natural més gran que 20.161 es pot descompondre com a suma de dos nombres abundants.

Igualment, Nicòmac també va definir en el seu tractat el nombre deficient, és a dir, aquell nombre natural que és major que la suma dels seus divisors propis. Per exemple el número 21 és un nombre deficient, ja que els seus divisors propis són 1, 3, 7 i que sumats s’obté 11 (1+3+7 = 11), que efectivament és menor que 21. Destaquem també que tots els nombres primers són deficients.

I per acabar, en l’aritmètica de Nicòmac també podem trobar curioses relacions numèriques, i que tant m’agraden, entre les quals destaca que:

“Qualsevol cub es pot expressar com a diferència de dos quadrats”, la qual cosa formalment s’expressa com a:

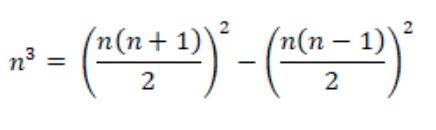
D’aquesta manera podem escriure:

2³ = 3² - 1², 3³ = 6² - 2, 4³ = 10² - 6², 5³ = 15² - 10², 6³ = 21² - 15²,… T

Imatge de capçalera: Generada per IA.