Les característiques generals dels arbres filogenètics
Un arbre filogenètic és una estructura matemàtica que permet modelitzar les relacions de parentiu entre un grup d’organismes o entre unes determinades seqüències de DNA, RNA o proteïnes.
De manera genèrica, les entitats que es comparen reben el nom d’UTO, acrònim d’Operational Taxonomic Unit (‘unitat taxonòmica operativa’). Malgrat que la terminologia que es fa servir en la construcció i la interpretació dels arbres pot variar una mica entre els diferents autors, hi ha determinats conceptes bàsics que s’empren de forma general.
La morfologia interna dels arbres filogenètics
En un arbre filogenètic es poden reconèixer nodes, ramificacions i, en alguns casos, l’arrel.
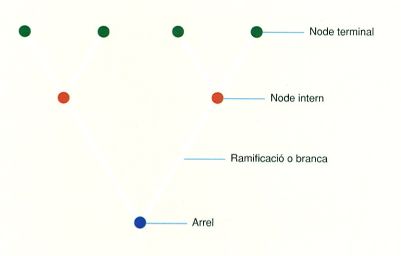
Terminologia bàsica dels arbres filogenètics. El node terminal és la seqüència o l’organisme real (actual o fòssil) els caràcters del qual s’analitzen, mentre que el node intern és l’ancestre hipotètic. L’arrel és l’ancestre de totes les seqüències o organismes dels nodes terminals.
Original de l’autor.
Per a començar, cal distingir entre genealogia i filogènia. Els arbres genealògics mostren qui descendeix de qui, i els ancestres s’hi identifiquen individualment. Els arbres filogenètics, en canvi, mostren qui és parent de qui, i no identifiquen els ancestres concrets, sinó que els reconstrueixen a partir de les dades dels llinatges que en parteixen, com un trencaclosques incomplet.
Un arbre és format per nodes connectats per ramificacions. Els nodes terminals, que també es poden anomenar fulles, tàxons terminals o UTO, representen les seqüències o els organismes actuals o fòssils dels quals s’analitzen els caràcters. És a dir, representen entitats reals. Els nodes interns, en canvi, representen els ancestres hipotètics a partir dels quals se separen els llinatges que van conduint, progressivament, cap als nodes terminals. L’ancestre de totes les seqüències o organismes que s’han inclòs als nodes terminals és l’arrel de l’arbre. Els nodes i les ramificacions poden contenir diversos tipus d’informació associada. Per exemple, hi ha mètodes de reconstrucció filogenètica que es basen en la reconstrucció seqüencial dels caràcters dels hipotètics ancestres en tots els nodes, com l’anomenat mètode de màxima parsimònia. Altres també estimen la quantitat d’evolució que s’ha produït entre un node i el següent, un valor que queda representat en la longitud de les ramificacions.
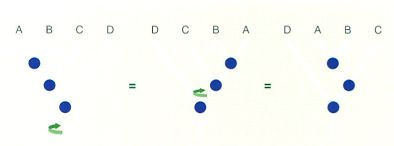
Diferents maneres de representar un mateix arbre filogenètic de quatre UTO (de la A a la D) sense que se n’alteri el significat ni la informació que conté. S’indica la direcció del gir de l’eix que genera cadascun dels arbres consecutius.
Original de l’autor.
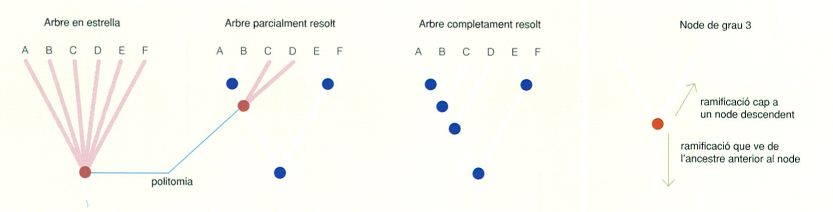
Tres graus de resolució d’arbres filogenètics, en exemples hipotètics de sis UTO (de la A a la F): des d’una manca completa de resolució (arbre en estrella, amb politomia total) fins a un arbre completament resolt, sense cap politomia. A la dreta, interpretació dels diferents graus dels nodes.
Original de l’autor.
D’un node poden sortir diverses branques. El nombre de branques adjacents que surten d’un node intern determina l’anomenat grau del node. Tots els nodes interns tenen una única ramificació cap a un node anterior, que determina el llinatge del qual precedeixen, però en canvi d’ells en poden sortir, teòricament, dues o més ramificacions que l’uneixen als seus descendents immediats. Per exemple, si un node és connectat a un node filogenèticament anterior per una ramificació, i en surten dues ramificacions cap a nodes posteriors, el seu grau serà 3 (1 + 2 = 3). En aquest context, si un node té un grau superior a tres, és a dir, si presenta més de dos descendents immediats, es diu que és un node politòmic. Es considera que els arbres que presenten politomies no estan completament resolts.
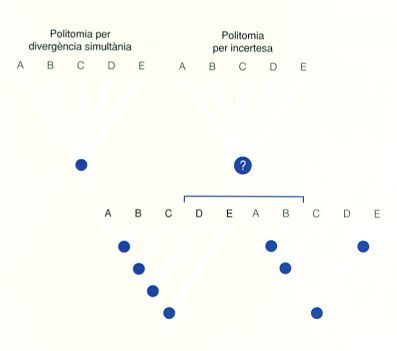
Dos tipus de politomia en arbres hipotètics de cinc UTO (de la A a la E): per divergència simultània (una situació molt poc freqüent) i associada a relacions filètiques incertes. En el darrer cas, s’indiquen dues de les possibles solucions de resolució de la incertesa.
Original de l’autor.
Les politomies poden representar dues situacions diferents. D’una banda, poden indicar una divergència simultània de llinatges; és a dir, que tots els descendents van evolucionar en el mateix moment a partir d’aquell avantpassat hipotètic. Alternativament, indiquen incerteses quant a les relacions filètiques; és a dir, que amb les dades de què es disposa no es té la certesa de quin és l’ordre correcte de les ramificacions, no pas que aquestes siguin simultànies. La major part de politomies pertanyen a aquesta segona categoria. Per aquest motiu les politomies indiquen que l’arbre en qüestió no està encara completament resolt.
Hi ha moltes maneres de dibuixar els arbres. Hi ha casos en què aquestes diferències porten implícits significats diferents quant a llur interpretació o a la informació que contenen, però sovint només obeeixen a convencions d’estil. Per exemple, l’ordre en què es representa un arbre pot diferir sense que això impliqui diferències en el seu significat. Aquest fet es produeix perquè els extrems de l’arbre poden rotar lliurement sense que s’alterin les relacions filogenètiques que s’hi representen.
L’arrel dels arbres
Els arbres es poden construir amb arrel o sense arrel. Els arbres amb arrel contenen un node particular, el de l’arrel, que representa l’ancestre comú de totes les UTO (organismes o seqüències) que s’estudien. És a dir, que determina una direcció evolutiva. Els arbres sense arrel, en canvi, només especifiquen les relacions de parentiu entre les UTO que s’analitzen, sense definir cap camí evolutiu.
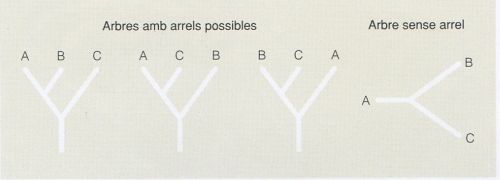
Tanmateix, partint d’un mateix nombre d’UTO, el nombre d’arbres amb arrel de topologia diferent que es poden inferir sempre és superior al d’arbres sense arrel, atesos els diferents camins evolutius que poden anar de l’arrel als diversos nodes terminals. Per exemple, si hom intenta agrupar tres espècies, podrà generar fins a tres arbres amb arrel diferents, però només un arbre sense arrel. Tant el nombre d’arbres amb arrel com el nombre d’arbres sense arrel que es poden generar donat un nombre determinat d’UTO és definit matemàticament.
Arbres veritables i arbres inferits
La possibilitat de realitzar diversos arbres filogenètics per a inferir les relacions de parentiu entre unes mateixes UTO contrasta amb l’obvietat que la seqüència de successos evolutius que ha conduït a la formació de cada grup terminal concret sigui històricament única. Això implica que només un dels molts possibles arbres que es poden construir ha de ser el veritable. Així, fins que hom no assoleix la construcció d’un arbre veritable es parla d’arbres inferits (o d’inferències filètiques).
Cladogrames, arbres additius i dendrogrames

Comparació entre un cladograma, un arbre additiu i un dendrograma, que estableix la relació de parentiu entre quatre UTO hipotètiques (de la A a la D). En el cladograma, A i B comparteixen un ancestre comú recent més proper que amb C. A i B formen un clade, juntament amb el seu darrer ancestre comú. I també formen un clade A, B, C i D, amb l’ancestre comú a tots quatre. A i C no formen un clade, atès que exclouen dos dels altres descendents (B i D). S’indiquen les equivalències entre arbres. Els nombres associats a les branques de l’arbre additiu quantifiquen el canvi evolutiu. En el cladograma i en l’arbre additiu l’eix vertical no té cap significat; en el dendrograma, Ma són milions d’anys. L’eix horitzontal no té cap significat en cap dels tres casos.
Original de l’autor.
Per a representar diversos aspectes de la filogènia dels organismes, es poden emprar diferents tipus d’arbres. L’arbre més bàsic conceptualment és el cladograma. El cladograma mostra la relació de parentiu dels organismes o seqüències que s’analitzen respecte al seu ancestre comú més recent. Per exemple, si es parteix de tres UTO concretes, A, B i C, el cladograma permet establir quines comparteixen l’ancestre comú més recent i quina té una relació de parentiu més allunyada. En aquest context, s’anomena clade un grup d’organismes descendents d’un ancestre comú, amb la condició que aquest grup inclogui tots els organismes que descendeixen d’aquest ancestre. El mètode de classificació basat en clades és la cladística.
Els arbres additius, en canvi, contenen informació addicional, concretament en la longitud de les branques. Aquesta longitud duu associada informació numèrica que quantifica el canvi evolutiu (però no el temps de divergència evolutiva). Per exemple, si un organisme presenta més substitucions de nucleòtids respecte al caràcter molecular analitzat que un altre amb què comparteix un ancestre comú, la seva branca en l’arbre serà més llarga. Per aquest motiu, en els arbres additius, la distància que hi ha entre els diferents nodes terminals i l’arrel no és sempre la mateixa, en funció de la quantitat de canvi evolutiu que dugui associada.
Finalment, els dendrogrames (que també s’anomenen arbres ultramètrics) són un tipus especial d’arbre additiu en què les puntes de les branques són totes equidistants respecte a l’arrel de l’arbre. Aquest tipus d’arbre s’utilitza per a representar el temps evolutiu, expressat directament en anys o indirectament a través de la divergència entre seqüències, utilitzant el concepte de rellotge molecular.
Així, mentre que els cladogrames contenen la informació suficient per a inferir els aspectes necessaris sobre els ancestres comuns i les relacions de parentiu dels organismes analitzats respecte a aquests ancestres, per a altres aspectes com la determinació de la taxa o el temps d’evolució cal emprar arbres additius o dendrogrames. Tots aquests arbres es poden representar també en forma circular.
Ancestres, fòssils vivents i formes intermèdies

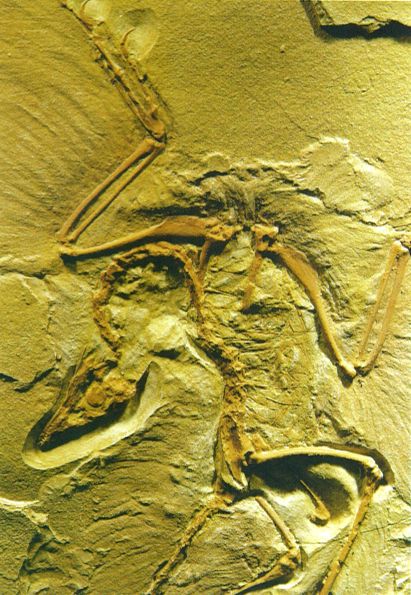
El celacant (a dalt) i l’Archaeopteryx (a baix) representen dos tipus diferents d’ancestres. El celacant (Latimeria chalumnae) és un fòssil vivent propi de les illes Comores morfològicament idèntic a determinats fòssils del Cretaci superior, malgrat el llarg període d’evolució. Archaeopteryx representa una forma intermèdia, que mostra caràcters típics dels dinosaures tetràpodes i d’altres propis dels ocells moderns, però en filogènia no se’l pot considerar un ancestre perquè no se’l pot situar en cap node intern concret.
Todd Huffman i iStockphoto.
La qüestió dels ancestres mereix una reflexió específica per emfasitzar que són hipotètics. En principi, hom podria pensar que els fòssils, els fòssils vivents o les formes intermèdies podrien ocupar aquest lloc en els arbres filètics, és a dir, que podrien representar els ancestres que ocupen la posició dels nodes interns. Els fòssils són les restes o senyals de l’activitat d’organismes del passat, i en filogènia no ocupen cap node intern, sinó que se situen en nodes terminals, com les formes actuals, al final de llurs respectius llinatges. Així, cal considerar que les formes actuals i les fòssils comparteixen ancestres comuns, a partir dels quals van divergir.
Respecte als fòssils vivents, són organismes actuals morfològicament idèntics a un fòssil conegut. Per exemple, el celacant o latimèria (Latimeria chalumnae) és un peix osteïcti que presenta unes extremitats relativament semblants quant a estructura interna a la dels tetràpodes, i la forma del qual és idèntica a determinats fòssils del Cretaci superior. Tanmateix, que siguin idèntics no implica que pertanyin a la mateixa espècie, atès que el llinatge que ha conduït a la forma viva actual ha estat sotmès a un llarg període d’evolució. En aquest sentit, malgrat que l’aparença morfològica hagi restat estable, la diferència genètica global pot ser significativa, ja que la morfologia dels vertebrats és controlada per menys del cinc per cent del genoma. Com en el cas dels fòssils, i malgrat que resulti temptador situar els fòssils vivents com el celacant al node intern que condueix cap als vertebrats tetràpodes, en filogènia els fòssils vivents no representen pas cap node intern, sinó que se situen en el node terminal del seu llinatge i es considera que comparteixen ancestres comuns amb les formes fòssils a les quals s’assemblen.
Finalment, hom es refereix a formes intermèdies per a designar aquells organismes, actuals o fòssils, que presenten característiques de dos o més llinatges diferents, com una mena de mosaic original. Per exemple, l’Archaeopteryx és un organisme intermedi, atès que té característiques típiques dels dinosaures tetràpodes, com ara una cua amb vèrtebres òssies, dents, l’estèrnum pla i ungles a les extremitats anteriors, i també característiques pròpies dels ocells moderns, com plomes, ales i espoletes. Aquestes formes intermèdies, però, tampoc no són els ancestres hipotètics que representen els nodes interns, sinó que en les anàlisis filogèniques se situen en nodes terminals, potser relativament a prop d’un node intern si hom té en compte les distàncies evolutives, però no pas en el node intern mateix.
En resum, en filogènia l’estat d’ancestre no es pot atorgar a cap forma actual ni fòssil. Són formes hipotètiques, les característiques de les quals es dedueixen a partir de la morfologia i de les dades moleculars dels organismes actuals i fòssils.
Arbres gènics i arbres d’espècies
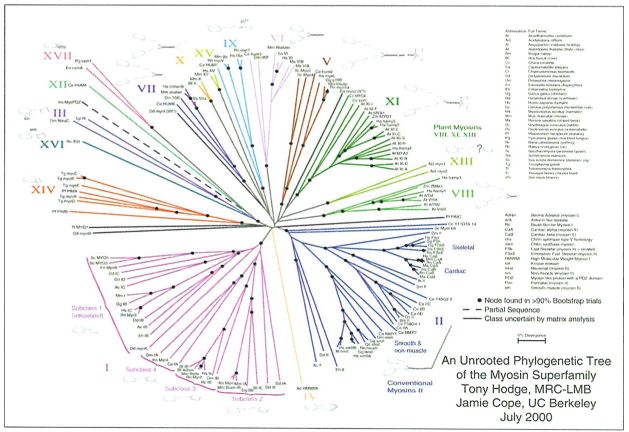
Arbre gènic sense arrel de la superfamília de la miosina, una proteïna contràctil present en tots els metazous. En aquest arbre no es representa la filogènesi d’un grup d’organismes, sinó la de diverses seqüències del gen de la miosina, que han estat obtingudes d’un gran ventall d’organismes (miosines ortòlogues) i també de diverses miosines d’un mateix organisme (miosines paràlogues).
Hodge i Cope, 2000.
Arbre de la vida basat en la seqüència completa del genoma dels organismes que s’hi esmenten. L’arrel d’aquest arbre circular indica l’origen de la vida.
Letunic, 2007.
Finalment, en funció de les UTO que es comparen, cal distingir entre dos tipus generals d’arbres. Si l’arbre representa les relacions de parentiu entre un grup concret d’espècies, s’anomena arbre d’espècies. En canvi, si es construeix per comparar el parentiu d’uns determinats gens ortòlegs i/o paràlegs, s’anomena arbre gènic. Els arbres d’espècies i els arbres gènics no han de coincidir necessàriament atès que, generalment, els gens comencen a divergir abans que se separin els llinatges, la qual cosa compromet qualsevol estimació que es vulgui fer del temps de divergència entre els llinatges. Tanmateix, aquest aspecte no representa un problema seriós quan s’analitzen llinatges que van divergir fa molt de temps.
A més, com ja s’ha esmentat en apartats anteriors, la taxa de canvi depèn de cada organisme i també de cada seqüència concreta de DNA. Per aquest motiu, per a fer reconstruccions filogenètiques dels organismes, és necessari emprar dades de diverses seqüències.
Els grups taxonòmics segons el seu origen filètic
Com s’ha dit en altres apartats, un tàxon és un grup d’organismes que, d’acord amb determinats criteris, es considera que formen una unitat, com per exemple una espècie, un gènere, una família, etc. Generalment als tàxons se’ls assigna un nom i una categoria, de tal manera que hom pot establir tàxons de categoria superior que engloben un o diversos tàxons de categoria inferior. Els arbres filogenètics es nodreixen de la taxonomia, al mateix temps que contribueixen a definir les seves agrupacions mitjançant les relacions de parentiu que estableixen.
Parafília, polifília i monofília
No tots els grups taxonòmics són igualment vàlids en la reconstrucció d’arbres. Així, hom distingeix tres tipus de grups taxonòmics en funció de l’origen filogenètic dels organismes que els formen. Concretament cal tenir en compte si cada grup taxonòmic concret inclou o no l’ancestre comú de tots els organismes que el constitueixen, i si tots els descendents d’aquest ancestre formen part del mateix grup taxonòmic. En funció d’aquests dos paràmetres els grups taxonòmics poden ser parafilètics, polifilètics o monofilètics.
Els grups parafilètics

L’arbre filogenètic de les angiospermes mostra que, si es contraposen les monocotiledònies a les dicotiledònies (en groc), aquest darrer grup es converteix en parafilètic: malgrat que inclou l’ancestre comú de tots dos grups, no conté tots els descendents (perquè exclou les plantes amb un sol cotilèdon).
A partir de fonts diverses
Un grup taxonòmic és parafilètic si conté l’avantpassat comú a tots els organismes que el formen, però en canvi només conté alguns dels descendents d’aquest avantpassat; és a dir, que alguns dels descendents d’aquest ancestre comú han estat inclosos en altres grups taxonòmics distints al que s’estudia. Tradicionalment, la major part de grups parafilètics s’han definit d’acord amb caràcters plesiomòrfics o simplesiomòrfics (similituds ancestrals) en lloc de fer-ho segons sinapomorfies (similituds derivades). Moltes de les classificacions tradicionals es basen en grups parafilètics. Alguns dels molts exemples de grups parafilètics que han bastit aquestes classificacions són: l’ordre dels artiodàctils (mamífers herbívors amb un nombre parell d’unglots a les extremitats, com el porc senglar, el cérvol i l’isard), atès que la taxonomia clàssica n’ha exclòs els cetacis, els quals filogenèticament són descendents d’un avantpassat comú pertanyent al mateix grup dels artiodàctils; el grup dels crustacis, atès que exclou els hexàpodes (un grup d’artròpodes que inclou la classe dels insectes) i l’avantpassat dels hexàpodes pertany al grup dels crustacis; el grup dels invertebrats definits com tots els animals sense vertebres, atès que exclou els vertebrats i aquests metazous procedeixen d’un ancestre invertebrat; el grup de les dicotiledònies definides en sentit clàssic (plantes amb dos cotilèdons), atès que les monocotiledònies en deriven. En aquest sentit, la filogènia molecular agrupa la major part de dicotiledònies dins el clade de les eudicotiledònies, però algunes dicotiledònies clàssiques queden en altres grups més basals, com els de les amborel·làcies, les nimfàcies o les magnòlides, entre d’altres, i per tant, si hom contraposa monocotiledònies a dicotiledònies, converteix aquest darrer grup en parafilètic, atès que exclou les plantes amb un sol cotilèdon.
Els grups polifilètics

Arbre filètic que mostra la polifília dels voltors. Malgrat que les semblances pel que fa a característiques morfològiques i etològiques són evidents, les han adquirides a partir d’ancestres diferents: és un cas típic d’evolució convergent. El node vermell indica la posició de l’ancestre comú a tots els voltors del Nou Món, i el node blau, el dels voltors del Vell Món. D’aquests respectius avantpassats comuns també deriven altres llinatges d’ocells amb característiques morfològiques i etològiques diferents que no són voltors, com els ocells de presa i les cigonyes.
A partir de Page i Holmes, 1998 / Corel i PhotoDisc / Jeremy Woodhouse
En canvi, un grup taxonòmic és polifilètic si inclou organismes d’origen filogenètic diferent, és a dir, que llur darrer ancestre comú no forma part del grup en qüestió. Moltes de les classificacions tradicionals també han pres com a base determinats grups polifilètics, per exemple, el grup dels animals homeoterms, atès que inclou els ocells i els mamífers, els quals no comparteixen cap ancestre comú recent que pertanyi en exclusiva a aquest hipotètic i no natural grup dels homeoterms; el grup dels voltors, atès que inclou dos llinatges independents d’ocells, els voltors del Nou Món i els del Vell Món (com per exemple, el voltor comú, Gyps fulvus, present als Països Catalans), els quals han adquirit de manera independent característiques morfològiques i etològiques similars, però a partir d’ancestres diferents.
Els grups monofilètics
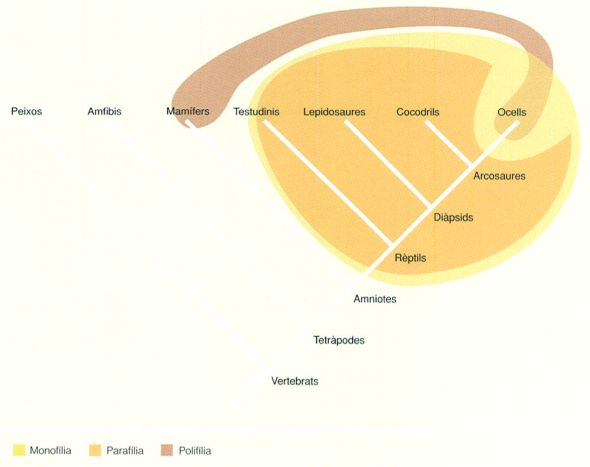
Arbre filètic simplificat dels vertebrats en què es mostren algunes de les relacions clàssiques de monofília, parafília i polifília. Els descendents del darrer ancestre comú a tots els rèptils constitueixen un grup monofilètic (en groc), el qual, per a poder ser considerat realment monofilètic, ha d’incloure necessàriament els ocells. En aquest sentit, si s’exclouen els ocells es converteix automàticament en parafilètic (en taronja), atès que deixa d’incloure tots els descendents d’aquest ancestre comú. I el grup dels metazous homeoterms és polifilètic (en marró), atès que els ocells i els mamífers no comparteixen cap ancestre comú recent exclusiu. També es pot apreciar que els ocells i els cocodrils constitueixen un clade natural, el dels arcosaures.
A partir de fonts diverses.
Finalment, un grup taxonòmic és monofilètic quan totes les espècies que conté comparteixen un ancessor comú que forma part d’aquest grup, i a més també engloba totes les espècies que en descendeixen. Els grups monofilètics es caracteritzen per compartir caràcters derivats, és a dir, sinapomorfies específiques. En cladística, les anàlisis filogenètiques s’han de basar en grups monofilètics.
La cladística i la fenètica
El propòsit dels estudis filogenètics és establir les relacions de parentiu entre les diverses espècies, agrupades en clades naturals. Un clade es defineix com un grup d’espècies o organismes que comparteixen un ancestre comú, el qual no és compartit per cap altra espècie fora del clade. Per tant, els clades són grups monofilètics. El mètode de classificació taxonòmica basat en la construcció de clades s’anomena cladística. I els arbres filogenètics basats en clades naturals s’anomenen cladogrames. Per exemple, com s’ha dit, el grup dels rèptils entès en sentit clàssic no és monofilètic, atès que no inclou els ocells, per la qual cosa no constitueix un clade natural. En canvi, per exemple, els ocells i els cocodrils sí que constitueixen un clade natural, el dels arcosaures, ja que comparteixen un ancestre comú no compartit per cap altre grup d’organismes, a la ramificació de llurs respectius llinatges.
Durant temps hi ha hagut una certa controvèrsia entre la cladística i la fenètica. La fenètica és l’estudi de les relacions entre un grup d’organismes pel seu grau de similitud, ja sigui morfològica, fisiològica o molecular. Els arbres que expressen relacions fenètiques s’anomenen fenogrames. En canvi, la cladística també inclou l’estudi dels camins evolutius o, dit d’una altra manera, quantes ramificacions filogenètiques presenta cada grup d’organismes, quines són les branques que es connecten en cada node i quina és la seqüència de ramificacions en un llinatge determinat. Els fenogrames poden ser utilitzats com a indicadors de relacions cladístiques, però no han de ser necessàriament coincidents amb els cladogrames. Tanmateix, si hi ha una relació lineal entre el temps de divergència dels llinatges i el grau de divergència morfològica i/o genètica, llavors els dos tipus d’arbres esdevenen idèntics.
Mètodes de reconstrucció i característiques particulars dels arbres filogenètics
Per a construir arbres filogenètics es poden emprar diversos mètodes, els quals generen arbres cladístics o fenètics en funció de cada mètode. Per exemple, el mètode anomenat de la màxima parsimònia genera arbres cladístics, mentre que l’anomenat UPGMA reconstrueix arbres fenètics. Altres mètodes, en canvi, com el d’unió de veïnatge, no es poden classificar fàcilment segons aquests criteris.
Una classificació més útil dels mètodes de reconstrucció d’arbres és la que distingeix els mètodes que es basen en distàncies evolutives o de canvi respecte als que es basen en l’estat concret de cada caràcter. Els primers estimen la distància o divergència evolutiva, per exemple, quantificant el nombre de substitucions aminoacídiques o nucleotídiques. Els segons, en canvi, analitzen quins nucleòtids o aminoàcids concrets hi ha en una posició determinada, o la presència d’insercions, delecions o transposicions específiques. Els primers tenen l’avantatge de fer servir grans quantitats de dades, i els segons, d’emprar-les de manera més selectiva. En tots dos casos, però, s’utilitzen matrius per a calcular els valors necessaris.
La generació de matrius

Passos essencials per a dur a terme la reconstrucció d’un arbre filogenètic amb caràcters moleculars, a partir de seqüències de DNA.
Original de l’autor.
Com s’ha dit en un apartat anterior, la construcció d’arbres filogenètics segueix una sèrie de passos. En el cas de la filogènia molecular, són els següents: en primer lloc, s’han d’escollir les seqüències d’interès, nucleotídiques o aminoacídiques; segonament, cal identificar les molècules homòlogues, mitjançant llur seqüenciació amb les tècniques adequades o bé descarregant-les d’un banc de dades pertinent si ja han estat seqüenciades amb anterioritat, com per exemple el GenBank, de l’NCBI dels Estats Units, el Nucleotide Sequence Database (EMBL) de la Unió Europea o el DNA Data Bank of Japan (DDBJ) del Japó; en tercer lloc, s’han d’alinear les seqüències amb determinades aplicacions bioinformàtiques, com per exemple, la plataforma BLAST; i finalment, cal fer els càlculs pertinents per inferir l’arbre filogenètic. A més, sovint també es combinen diversos tipus de dades moleculars i morfològiques, la qual cosa genera matrius certament complexes.
Primer, de manera general i simplificada, els programes d’alineació de seqüències fragmenten les seqüències que s’han d’alinear en fragments més curts, que en nomenclatura bioinformàtica s’anomenen paraules (o words), la longitud dels quals es pot determinar per ajustar la cerca segons convingui. Després busquen altres paraules similars en les altres seqüències, alineen totes les molècules d’aquests fragments en funció de la seva similitud, i comparen i quantifiquen aquesta similitud mitjançant una matriu de substitucions. Les matrius de substitucions són unes taules que permeten quantificar tots els possibles parells correctament alineats. En el cas del DNA, per exemple, normalment s’assigna un valor +1 als nucleòtids aparellats que són iguals, i 0 als que són diferents.

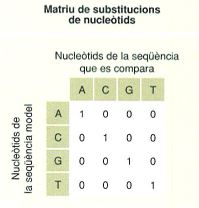
Matriu de substitucions nucleotídiques (a l’esquerra) i de substitucions aminoacídiques (a la dreta). En la segona, cada posició en una proteïna pot ser ocupada per un dels 20 aminoàcids (escrits segons el codi d’una lletra) i la magnitud del canvi (la probabilitat que es fixi i pugui ser observat) depèn de la seva afinitat química. Per això, el sector emmarcat en vermell comprèn els valors de diferència. Aquesta matriu concreta s’anomena BLOSUM62.
Henikoff i Henikoff, 1992.
Si es treballa amb seqüències d’aminoàcids, la quantificació de la similitud és més complexa, perquè hi ha 20 aminoàcids diferents que poden ocupar cada posició concreta en la proteïna (en el cas dels àcids nucleics únicament hi ha 4 nucleòtids). A més, en aquest cas es poden utilitzar dos mètodes de quantificació. Un té en compte la similitud química dels aminoàcids, atès que si un aminoàcid és substituït per un altre amb unes característiques químiques similars, la funció global de la proteïna es veurà menys afectada que si és substituït per un que té unes característiques químiques completament diferents, la qual cosa influeix sobre la probabilitat que el canvi es fixi i, en conseqüència, que es pugui observar. L’altre mètode, en canvi, té en compte probabilitats conegudes de les diferents substitucions observades en el decurs de l’evolució.
A partir d’aquestes dades, els algoritmes alineen les seqüències a la recerca de l’aparellament que presenta més similituds. Un cop s’ha alineat correctament una paraula, l’algoritme estén l’alineació cap a la resta de seqüència. En aquest procés, a més de poder-se determinar la mida de les paraules, també es pot determinar el tipus de matriu de substitució que s’ha d’utilitzar i el llindar a partir del qual es vol que la similitud resulti suficient per a considerar una hipòtesi d’homologia. I també es contempla la possibilitat d’introduir espais buits (gaps, en terminologia bioinformàtica) per suplir les molècules que falten en aquells indrets de la molècula on s’ha produït una inserció o una delectó, ja que altrament seria impossible considerar la resta de similituds de la cadena nucleotídica o aminoacídica. Aquests espais buits s’omplen amb guionets, als quals també es poden assignar determinats valors per a la quantificació total final de similitud.

Alineació i quantificació de la similitud entre una seqüència de nucleòtids model (una paraula, en terminologia bioinformàtica) i dues hipotètiques seqüències homòlogues (#1 i #2).
Original de l’autor.

Homologia entre dues seqüències de DNA en què hi ha hagut una inserció o una deleció. A dalt, no es considera la possibilitat d’introduir espais buits per suplir les insercions o delecions i l’homologia és molt menor. A baix, no s’han considerat possibles puntuacions associades als gaps. En totes dues alineacions es ressalten els nucleòtids aparellats.
Original de l’autor.
D’altra banda, hi ha algunes molècules concretes, com els RNAr i els RNAt, que presenten estructures tridimensionals específiques, les quals han de ser considerades a l’hora de fer les alineacions pertinents. Finalment, cal dir que aquests algoritmes, malgrat que alineen les seqüències i quantifiquen llur similitud, no poden identificar quins dels alineaments són rellevants per a la qüestió a resoldre. Això depèn, en bona part, del criteri dels investigadors, per la qual cosa a partir d’unes mateixes alineacions es poden desprendre relacions filogenètiques lleugerament diferents. La utilització d’un nombre suficient de seqüències, però, disminueix enormement les conseqüències d’aquesta possible font de variabilitat.
Els principals mètodes per a construir arbres

Síntesi dels principals mètodes filogenètics utilitzats en la reconstrucció d’arbres, classificats segons la base metodològica i el tipus de dades emprades.
Original de l’autor.
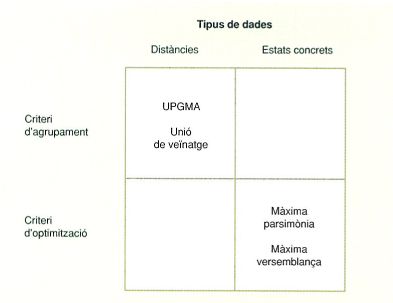
Hi ha dos tipus generals de mètodes per a construir arbres, que es basen en distàncies evolutives o alternativament en els estats concrets de cada caràcter.
Els mètodes que es basen en distàncies converteixen la matriu de caràcters en una matriu de distàncies, la qual representa la distància evolutiva entre totes les parelles d’UTO que s’estan analitzant. En aquest cas, l’arbre filogenètic es construeix amb algoritmes com el d’unió de veïnatge o amb el mètode UPGMA.
En canvi, els mètodes que es basen en els estats concrets de caràcters específics seleccionen l’arbre filogenètic que pot ser explicat amb el mínim nombre de canvis en els caràcters usats en la matriu. Dit d’una altra manera, seleccionen l’arbre que atorga la màxima probabilitat que es puguin observar aquelles dades en funció d’un model determinat. En són exemples el mètode de la màxima parsimònia i el de màxima versemblança.
El mètode UPGMA
Construcció d’un arbre filogenètic pel mètode UPGMA amb sis UTO (tàxons o seqüències) hipotètiques (de la A a la F).
A partir d’Opperdoes, 1997.
El mètode d’agrupació per parelles no ponderades amb mitjana aritmètica o UPGMA (de l’acrònim anglès Unweighted Pair Group Method with Arithmetic mean) és el mètode més senzill per a reconstruir arbres filogenètics. Inicialment es va desenvolupar per a construir fenogrames taxonòmics, però també es pot emprar per a inferir arbres filogenètics, amb la condició que les taxes d’evolució siguin aproximadament constants entre els diversos llinatges. Si es compleix aquesta condició, hom pot pressuposar una relació lineal entre la distància evolutiva i el temps de divergència. Aquest mètode fa servir un algoritme d’agrupament seqüencial, en el qual les relacions topològiques locals són idèntiques per a mantenir la similitud, i l’arbre es construeix de manera també seqüencial.
Dit d’una altra manera, primer identifica, entre totes les UTO que formen part de l’estudi, les dues que són més semblants, i les agrupa. Després, tracta aquesta agrupació com si fos una única UTO nova, i torna a repetir l’anàlisi per a identificar un altre cop les dues UTO més semblants, i les agrupa. Aquest cicle es repeteix de forma iterativa fins que totes les UTO estan agrupades.
Si les taxes evolutives no són constants, llavors es poden emprar determinats algoritmes que corregeixen les distorsions topològiques, com per exemple l’anomenat mètode de transformació de distàncies.
El mètode d’unió de veïnatge

Construcció d’un arbre filogenètic pel mètode d’unió de veïnatge amb sis UTO (tàxons o seqüències) hipotètiques (de la A a la F).
A partir d’Opperdoes, 1997.
El mètode d’unió de veïnatge (neighbour joining) utilitza un algoritme que identifica les UTO veïnes per a generar arbres sense arrel. En un arbre bifurcat sense arrel, es diu que dues UTO són veïnes si estan connectades per un únic node intern. En aquest context, el mètode d’unió de veïnatge computa primer una matriu de distàncies com la que es fa amb l’UPGMA. Llavors agafa totes les combinacions possibles de quatre UTO, fa totes les combinacions possibles d’aquestes UTO agafades de dues en dues i calcula llurs distàncies. Després de fer això per a totes les possibles combinacions de quatre UTO, selecciona el parell d’UTO que tenen un valor de distància menor i les agrupa, i des d’aquell moment les considera com si fossin una sola UTO. A continuació construeix una nova matriu de distàncies incloent-hi aquesta nova UTO, i el cicle torna a començar.
Aquest mètode, que és estadísticament consistent i que amb molta probabilitat genera arbres veritables, es basa en el criteri de mínima evolució, segons el qual l’arbre que se selecciona és el que en cada pas de la seva construcció genera unes branques més curtes (i la longitud de la branca és un indicatiu del grau d’evolució). Tanmateix, el fet de construir-se de manera seqüencial fa que la topologia final de l’arbre no hagi de ser necessàriament l’òptima per a descriure aquella filogènia. La seva gran virtut, en canvi, és la seva gran eficiència computacional.
Altrament, a diferència de l’UPGMA, no considera que tots els llinatges hagin de tenir la mateixa taxa d’evolució, i, com s’ha dit, produeix arbres sense arrel. Tanmateix, si es vol generar un arbre amb arrel emprant aquest mètode, n’hi ha prou d’incorporar a l’anàlisi un grup filogenèticament extern. Llavors, el punt d’embrancament d’aquest grup extern amb els que s’estan analitzant situa l’arrel de l’arbre.
El mètode de màxima parsimònia
El mètode de la màxima parsimònia (maximum parsimony) és un mètode estadístic no paramètric que, donades diverses UTO, identifica l’arbre que requereix el nombre mínim de canvis evolutius per a explicar les diferències observades en les UTO que s’estudien. Tanmateix, sovint, en aplicar els algoritmes corresponents, s’obtenen diversos arbres que satisfan aquest criteri, per la qual cosa no sempre és possible inferir un arbre únic.
En aquest mètode, primer cal identificar els llocs informatius de les UTO que s’analitzen. Així, per exemple, es considera que una posició només és filogenèticament informativa si afavoreix alguns d’aquests possibles arbres sobre la resta. És a dir, una posició és informativa si hi ha com a mínim dues molècules diferents en aquell lloc quant a les diferents UTO, i si cadascuna és present com a mínim en dues de les seqüències que s’estan comparant.
Un cop identificats els llocs informatius, aquest mètode construeix tots els arbres possibles i calcula per a cadascun el nombre de substitucions per cada lloc informatiu que els justifica. Finalment, suma totes les substitucions i selecciona l’arbre que s’ha generat amb un nombre mínim d’aquestes substitucions.
El mètode de màxima versemblança
Finalment, el mètode de màxima versemblança (maximum likelihood) es basa en la selecció, d’entre tots els arbres filogenètics possibles que relacionen les UTO que s’estudien, d’aquell que fa que les dades observades siguin les més probables d’haver esdevingut. O, dit d’una altra manera, selecciona els paràmetres del model que maximitzen la probabilitat que evolutivament s’hagin generat les dades que hom observa. La principal virtut d’aquest mètode és que permet incorporar models explícits d’evolució seqüencial i també permet realitzar tests estadístics per a valorar les hipòtesis evolutives.
Els conflictes filogenètics: robustesa i arbres consens
Atesa la diversitat de mètodes que es poden fer servir per a generar arbres i la gran varietat i heterogeneïtat de caràcters que hom pot emprar per a obtenir les matrius corresponents, no és estrany que sovint es produeixin conflictes filogenètics, entesos com diferents respostes filogenètiques a una mateixa pregunta. És a dir, que a partir d’un mateix conjunt d’UTO es poden generar diversos arbres topològicament diferents.
Una altra causa d’aquests conflictes és el nombre d’organismes analitzats, un percentatge molt petit respecte al total d’organismes que formen la gran diversitat de la vida. O, vist al revés, l’acumulació de dades d’un nombre creixent d’organismes permet perfilar de manera cada cop més precisa i consistent els arbres filogenètics. Tanmateix, encara hi ha algunes relacions, àdhuc en nodes relativament basals de l’arbre de la vida, que no estan completament resoltes.
Avaluació objectiva dels mètodes de reconstrucció
Com s’ha esmentat diverses vegades, cada mètode de reconstrucció filogenètica té els seus avantatges i els seus desavantatges. Hi ha investigadors que, per principi, prefereixen uns determinats mètodes que d’altres. Així, n’hi ha que prefereixen el mètode de màxima parsimònia, mentre que d’altres advoquen pel de màxima versemblança. Els mètodes basats en distància es valoren especialment per la seva capacitat d’emprar qualsevol tipus de dada de manera relativament simple. No obstant això, aquests mètodes difereixen quant als fonaments conceptuals, i també en els resultats. Una anàlisi extensa d’aquests mètodes i dels avantatges respectius escapa al propòsit d’una Història Natural. Tanmateix hi ha diverses aproximacions possibles per a avaluar la consistència d’aquests mètodes i dels arbres que produeixen.
Un dels criteris pràctics per a avaluar els mètodes és la seva eficiència, entesa com llur rapidesa de funcionament. Malgrat que hom usi plataformes informàtiques, la major part dels mètodes exigeixen càlculs llargs, complexos i iteratius. Així, els mètodes de màxima versemblança i de màxima parsimònia són significativament més lents que els basats en distàncies, atès que en cada cicle han d’examinar i reexaminar tots els arbres que generen.
Un altre dels criteris d’avaluació dels mètodes és la consistència dels arbres que generen, és a dir, la fiabilitat quant a l’exactitud si hom utilitza un nombre suficient de dades. I un altre és la seva potència estadística a l’hora de validar o rebutjar les hipòtesis.
D’altra banda, malgrat que tots els mètodes filogenètics busquin les relacions de parentiu, fan assumpcions sobre els processos evolutius subjacents als canvis observats respecte als caràcters que s’analitzen. Atès que no sempre es coneix l’exactitud d’aquesta assumpció, també s’avalua el grau de dependència dels mètodes respecte a aquestes assumpcions, una característica que es coneix com a robustesa.
La robustesa és una manera de valorar l’error de mostreig, és a dir, de quantificar de manera objectiva fins a quin punt les conclusions o la topologia de l’arbre varien en funció de les mostres utilitzades. Això s’aconsegueix analitzant diverses vegades les mateixes mostres, o generant alternativament dades artificials a partir de les reals, inclòs el mateix arbre, i analitzant la seva coincidència amb el model. En tots els casos s’obtenen un valors, anomenats valors de bootstrap, que s’acostumen a posar al costat de cadascuna de les branques per a indicar-ne la robustesa.
El darrer criteri és el de la falsabilitat del mètode. La falsabilitat és l’assumpció que una teoria ha de poder ser refutada si hom fa una observació que la contradigui. Aplicada a la filogènia, la falsabilitat indica fins a quin punt els resultats permeten determinar si les assumpcions evolutives subjacents han estat violades. Aquest criteri és especialment important per als mètodes que no són gaire robusts.
Els arbres consens

Comparació entre un arbre construït per consens estricte i un de construït per consens majoritari, inferits a partir de tres arbres filogenètics hipotètics que relacionen les mateixes UTO, anomenades de la A a la E.
Original de l’autor.
Finalment, atès que en moltes ocasions un mateix conjunt d’UTO pot generar arbres amb certes diferències topològiques, cal combinar els resultats en un sol arbre, anomenat arbre consens. Un arbre consens representa els aspectes comuns d’un grup d’arbres que relacionen filogenèticament uns mateixos clades. O, dit d’una altra manera, és l’arbre que resumeix la informació comuna a dos o més arbres parcialment distints.
Per a construir arbres consens es poden emprar diversos mètodes, que es diferencien segons els aspectes dels arbres que es fan servir i en la freqüència que una determinada informació ha de trobar-se compartida entre els diversos arbres per a poder ser introduïda en el consens. Els mètodes més utilitzats són el de consens estricte, el de consens majoritari i el de consens d’Adams.
Els arbres de consens estricte només inclouen les agrupacions, les ramificacions i els nodes que es donen en tots els arbres considerats. La resta s’indiquen com a politomies, és a dir, com a aspectes no resolts de l’arbre.
Els arbres de consens majoritari, en canvi, consideren les agrupacions, les ramificacions i els nodes que es troben en més de la meitat dels arbres considerats. En aquest cas, al costat de cada ramificació de l’arbre de consens s’acostuma a indicar el percentatge d’arbres en què es dóna aquella ramificació concreta, com un valor de confidència.

Comparació entre un arbre construït per consens estricte i un de construït per consens d’Adams, inferits a partir de dos arbres filogenètics hipotètics que relacionen les mateixes UTO, anomenades de la A a la E.
Original de l’autor.
Finalment, els arbres per consens d’Adams es construeixen capturant les diverses informacions dels arbres considerats i representant-les de forma única. Sovint aquests arbres són difícils d’interpretar, però són molt útils en situacions en què una o més UTO tenen posicions molt diferents en els arbres que es comparen.