Resultats de la cerca
Es mostren 11 resultats
resultant
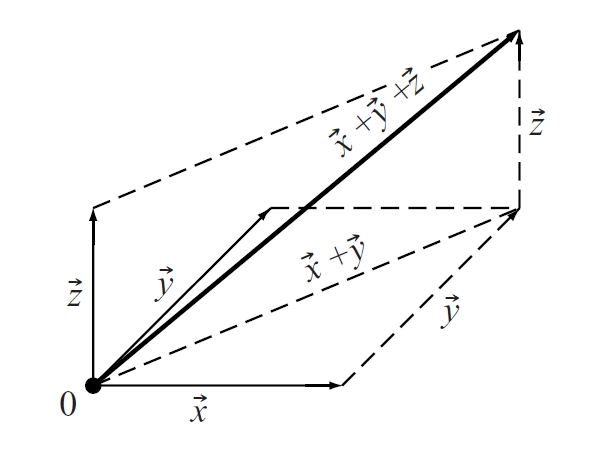
Resultant d’una suma de vectors
Física
Vector equivalent a la suma de dos vectors.
Donats dos vectors, hom n'obté la resultant per la regla del parallelogram cal construir un parallelogram que tingui per costats els vectors donats, i la resultant és aleshores la diagonal d’aquest parallelogram
sèrie de Brackett
Física
Conjunt de ratlles de l’espectre atòmic de l’hidrogen, que corresponen a les transicions al nivell de nombre quàntic principal n = 4; són a la part infraroja de l’espectre.
Els valors de les diferents longituds d’ona vénen donats per l’expressió 1/λ = R H 1/4 2 - 1/ N 2 , essent R H la constant de Rydberg per a l’àtom d’hidrogen R H = 109 737 cm -1 i N un nombre enter més gran que 4
sèrie de Balmer
Física
Conjunt de ratlles de l’espectre atòmic de l’hidrogen, que corresponen a les transicions al nivell de nombre quàntic principal n=2; són a la regió visible i a la de l’ultraviolat proper de l’espectre.
Els valors de les diferents longituds d’ona són donats per l’expressió l/λ= R H 1/2 2 -1/ N 2 , essent R H la constant de Rydberg per a l’àtom d’hidrogen R H =109 737 cm - 1 i N un nombre enter més gran que 2 Aquesta equació, deduïda empíricament per JJ Balmer, no rebé una interpretació teòrica correcta fins a l’adveniment del model de l’àtom de Bohr
xarxa de difracció
Física
Superfície transparent (plana) o reflectora (plana o còncava) on són gravades un seguit d’estries (o traços), rectilínies, idèntiques, paral·leles i equidistants i que hom empra generalment com a sistema dispersor de radiació policromàtica.
Si la superfície és plana hom parla de xarxa plana i, si és còncava, de xarxa còncava Les estries poden ésser gravades sobre una superfície transparent plana xarxa transmissora , o sobre una superfície metàllica, plana o còncava xarxa reflectora , o bé poden ésser les franges d’una imatge hologràfica impressionada sobre un material sensible xarxa hologràfica Hom empra també la xarxa esglaonada , en què les estries formen un perfil de dent de serra En el cas d’una xarxa transmissora, si una ona plana incideix sobre la seva superfície amb un angle d’incidència i , hom pot…
moment d’un vector respecte a una recta
Física
Donats un vector i una recta, component segons la recta del moment del vector respecte a un punt qualsevol de la recta.
Pot ésser demostrat que aquesta component no depèn del punt de la recta escollit En el cas que el vector representi una força, hom parla del moment de la força respecte a la recta Si, en comptes d’un únic vector, hi ha un sistema de vectors, hom anomena moment resultant del sistema de vectors respecte a la recta la suma dels moments de cadascun dels vectors respecte a la recta
moment angular respecte a un punt
Física
Donats una partícula en moviment i un punt arbitrari A, moment del vector moment lineal de la partícula respecte al punt A
.
El moment angular és anomenat també moment cinètic i quantitat de moviment angular i, en el cas d’un sistema de partícules, és definit com la suma dels moments angulars de les partícules del sistema La propietat que fa interessant el moment angular és establerta per l’anomenat teorema del moment angular , segons el qual, sota condicions molt generals com, per exemple, agafar el punt A fix, la derivada temporal del moment angular respecte al punt A és igual al moment resultant, respecte al punt A , del sistema de forces exteriors actuants Un corollari immediat d’aquest teorema és l’anomenat…
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un…
luminància
Electrònica i informàtica
Física
Donats un punt d’una superfície i una direcció determinada, quocient entre la intensitat lluminosa emesa en aquesta direcció per un element infinitament petit de la superfície al voltant del dit punt i l’àrea d’aquest element projectada ortogonalment sobre un pla perpendicular a la direcció donada.
La unitat SI de luminància és el nit, bé que també és emprat el stilb, el lambert o l’apostilb És la magnitud fotomètrica corresponent a la lluminositat
radiància
Electrònica i informàtica
Física
Donats un punt d’una superfície i una certa direcció, quocient entre la intensitat de radiació en aquesta direcció d’un element infinitament petit de la superfície que envolta el punt considerat i l’àrea de la projecció ortogonal de l’esmentat element sobre un pla normal a la direcció considerada.
És anomenada també luminància energètica o radiant