Resultats de la cerca
Es mostren 3270 resultats
funció conjugada d’una funció
Matemàtiques
Donada una funció f: D→ℂ, on D⊂ℝo D⊂ℂ, funció fD→ℂ definida per f( x)=f(x).
Òbviament, f és la funció conjugada de f f i f són mútuament conjugades
equació integral
Matemàtiques
Equació on la funció que cal determinar es troba dins l’integrant d’una certa integral coneguda.
L’exemple més simple és l’equació , on la funció f x és coneguda i cal trobar la funció f x En virtut del teorema fonamental del càlcul, la solució és, en certes condicions de regularitat, Aquestes equacions les trobem en la resolució matemàtica de problemes físics i tècnics
àlgebra tensorial
Matemàtiques
És, dins de l’àlgebra abstracta, una construcció d’una àlgebra associativa T(E) partint d’un espai vectorial V.
Sigui E un espai vectorial sobre un cos commutatiu K , per a cada parella p , q de nombres naturals, existeix una aplicació bilineal única T pq de T p E X T q E en T p+q E tal que, per a tot element x 1 ,, x p d’ E p i tot element x p+1 ,, x p+q d’ E q , T pq x 1 OOOoooOOO x p , x p+1 OOOoooOOO x p + q = x 1 OOOoooOOO x p+q , on T n E és la potència tensorial n -èsima d E Les aplicacions bilineals T pq defineixen sobre l’espai vectorial una estructura de K -àlgebra graduada És l’àlgebra tensorial de l’espai vectorial E i és designat T E
àlgebra graduada
Matemàtiques
Àlgebra sobre un cos, altrament conegut com R-àlgebra, en la qual hi ha una noció consistent del pes d’un element. La idea és que els pesos dels elements se sumin quan es multipliquen els elements tot i que ha de permetre l’addició ‘inconsistent’ de diversos pesos.
Àlgebra E sobre un cos commutatiu K que és suma directa d’una successió de subespais { E n n ∈ ℕ } i, per a cada parella p , q de nombres naturals, el producte d’un element d’ E p per un element d’ E q pertany a E p+q
test d’hipòtesis estadístiques
Matemàtiques
Donada una mostra de grandària n, ( x1,...,xn ), formada per n realitzacions o observacions independents d’un cert fenomen o experiment.
Aquest mètode permet de decidir, a partir de les dades observades, si una hipòtesi estadística que hom ha fet sobre el model probabilístic del fenomen és correcta o no ho és Aquesta decisió hauria d’ésser presa sempre amb un cert grau d’incertesa Els problemes que tracta de resoldre aquesta teoria poden ésser, per exemple, decidir quin dels dos mètodes diferents de fabricació de bombetes elèctriques dona una mida mitjana més gran, o bé saber, a partir d’una sèrie d’anàlisis, si un malalt té una certa malaltia Sovint el model probabilístic consisteix en una llei de probabilitat teòrica donada…
sèrie de potències
Matemàtiques
Donada una funció real de variable real f (x) derivable indefinidament en el punt x0, sèrie Σ an (x-x0)n amb an = (1/ n !) fn (x0).
Es compleix que f x = Σ a n x- x 0 n per a tots els punts x tals que | x- x 0 | < R, on R és el radi de convergència de la sèrie Aquesta sèrie és anomenada sèrie que desenvolupa la funció f en un entorn del punt x 0 , o sèrie de Taylor de f en el punt x 0 La sèrie de potències és utilitzada per a expressar el desenvolupament en sèrie d’una funció Així, per exemple, hom té la sèrie exponencial , que és convergent per a tot x
variació
Matemàtiques
Qualsevol successió de n elements d’un conjunt de cardinal m, els quals són diferents dos a dos.
El conjunt de totes les possibles variacions de m elements presos de n en n , V n m , té cardinal El quocient de V n m per les possibles permutacions dels n elements P n = n = n n -1 21, dona el nombre de combinacions C n m dels m elements presos de n en n combinació Hom pot repetir cada element un nombre de vegades qualsevol, i això dona lloc a les variacions amb repetició VR n m El nombre d’aquestes és donat per l’expressió VR n m = m n
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…
semblança
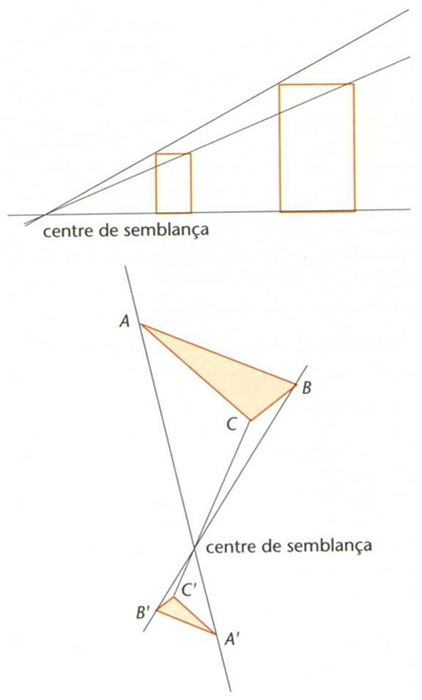
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament una…
Pablo Miquel Merino
Matemàtiques
Matemàtic.
Fill del català Pau Miquel i Costas, comerciant resident a l’Havana en el segle XIX A Cuba, estudià els primers estudis i el batxillerat, al Colegio de Belén Després d’aquesta etapa, passà tot seguit al País Basc, on estudià matemàtiques a la Universitat de Deusto Retornà a Cuba, on, el 1908, guanyà per oposició el càrrec d’ajudant facultatiu del gabinet d’astronomia Doctor en ciències fisicomatemàtiques, obtingué, el 1913, a la Universitat de l’Havana, la càtedra d’anàlisi matemàtica, on treballà durant més de 30 anys Entre la seva prolífica obra científica, cal destacar obres com Curso de…