Resultats de la cerca
Es mostren 166 resultats
conjunt de Borel
Matemàtiques
Qualsevol conjunt que pugui ésser obtingut a partir d’una col·lecció numerable de conjunts oberts o tancats a la recta real mitjançant un seguit numerable d’operacions d’unió, d’intersecció o de compleció.
funció generatriu d’un conjunt de funcions
Matemàtiques
Funció de dues variables f
( z,u
) tal que el seu desenvolupament en sèrie de potències respecte a una de les variables, p ex u
, té com a coeficients d’aquestes potències les funcions del conjunt en qüestió.
Així, la funció és la funció generatriu de les funcions de Bessel d’índex enter, J n z
variació
Matemàtiques
Qualsevol successió de n elements d’un conjunt de cardinal m, els quals són diferents dos a dos.
El conjuntde totes les possibles variacions de m elements presos de n en n , V n m , té cardinal El quocient de V n m per les possibles permutacions dels n elements P n = n = n n -1 21, dona el nombre de combinacions C n m dels m elements presos de n en n combinació Hom pot repetir cada element un nombre de vegades qualsevol, i això dona lloc a les variacions amb repetició VR n m El nombre d’aquestes és donat per l’expressió VR n m = m n
fractal
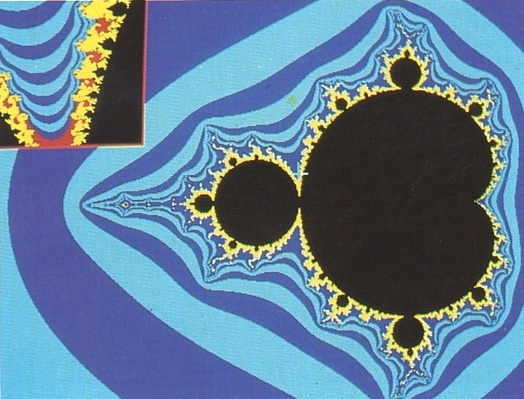
fractal Conjunt de Mandelbrot i un detall (corresponent al punt marcat per una creu blanca) [imatge obtinguda per ordinador al Departament d’Informàtica de la Universitat Autònoma de Barcelona]
Matemàtiques
Model matemàtic o objecte real que manté la seva forma essencial, fragmentada i irregular, tot i variant l’escala d’observació.
Les primeres fractals corbes de Von Koch, Peano, Sierpiński, etc aparegueren entre el 1875 i el 1925 com a contraexemples als intents de formalització de l’actual matemàtica Benoît Mandelbrot, els anys setanta, descobrí que aquests models serveixen per a representar la realitat Basant-se en els conceptes d’homotècia interna i de dimensió en el sentit de Hausdorff-Besikovič 1919, Mandelbrot definí les bases de la geometria fractal, que permet de modelitzar fenòmens com les turbulències, el cabal dels…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjuntde condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjuntde condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè…
permutació
Matemàtiques
Aplicació d’un conjunt de n elements a n llocs diferents, és a dir, cadascun dels diferents arranjaments lineals que es poden fer amb diferents elements, entrant tots ells en cadascun dels arranjaments.
El nombre de permutacions diferents que hom pot fer amb un conjuntde n elements és n n factorial i és donat per la fórmula n = n n- 1 n -2 2 × 1 Si hom identifica alguns dels elements del conjunt, obté les permutacions amb repetició Si el conjunt és identificat en classes de n 1 , n 2 n r elements, el nombre de permutacions amb repetició és n / n 1 n 2 n r Si hom suposa que els llocs són disposats en un cercle i que no es distingeix entre dues permutacions si només difereixen en una rotació…
independència lineal
Matemàtiques
En un espai vectorial E sobre un cos C, relació entre un conjunt de vectors, v1, ..., vn, tals que qualsevol combinació lineal igualada a zero, a1v1+...+anvn =0, implica que tots els coeficients són nuls, ai =0, i=1,...,n.
Els vectors v 1 ,,v n són aleshores linealment independents Un conjuntde vectors linealment independents pot ésser ampliat per tal de formar una base d’un espai vectorial La propietat oposada a la independència lineal és la dependència lineal