Resultats de la cerca
Es mostren 12 resultats
esperança
Matemàtiques
En un joc d’atzar, guany mitjà per jugada.
Un joc és dit equitatiu si la seva esperança és nulla
esperança matemàtica
Matemàtiques
Valor mitjà que pot prendre una variable aleatòria X definida en un espai de probabilitat (Ω, Q, P).
És la integral definida E X = ∫ XdP de la funció X relativament a la probabilitat P En el cas discret si on X i són valors reals i I A i els indicadors d’una partició { A i ,,A n } de l’espai, l’esperança pren el valor L’ esperança condicionada d’una variable aleatòria X , donat un esdeveniment A , és la integral definida
martingala
Matemàtiques
Procés estocàstic
de Markov {
X n
} que, a més de tenir una esperança matemàtica finita per a tot valor de t
, té una esperança condicionada
essent aquest el valor pres en l’instant
t n - 1
.
L’origen d’aquest nom prové de l’estudi dels jocs d’atzar quan hom vol descriure la fortuna d’un jugador immers en un sistema de jocs que són “neutres” en el sentit de l’esperança matemàtica
desviació mitjana
Matemàtiques
Esperança matemàtica del valor absolut de la diferència entre una variable aleatòria i la seva mitjana.
Si la mitjana de n mesures de la variable x és x , aleshores la seva desviació mitjana és 1/n
moment
Matemàtiques
Donada una variable aleatòria X, i f (x) essent la seva funció de densitat, valor mr donat per la fórmula
on a és un nombre real fixat i r és un nombre natural que determina l’ordre del moment.
Normalment hom escull com a valor de a el de l’esperança matemàtica de X , en el qual cas el moment de primer ordre és a dir r = 1 és nul i el de segon ordre és a dir, r = 2 coincideix amb la variància A partir dels moments, mitjançant l’anomenat mètode dels moments , hom pot estimar els paràmetres que caracteritzen una distribució de freqüències obtinguda a partir de l’observació d’una mostra
variància
Matemàtiques
Mesura de la dispersió d’una variable aleatòria X respecte al seu valor mitjà.
Hom la defineix mitjançant la següent igualtat σ 2 X = E X - E X 2 E X essent l’esperança matemàtica o valor mitjà de X La variància és, doncs, el moment de segon ordre corresponent a la variable X centrada La seva arrel quadrada σ és la desviació tipus En el cas discret, és a dir, si la variable aleatòria X pren un nombre finit de valors x 1 , …, x n amb probabilitats respectives P 1 , …, P n , aleshores hom té
teoria de la decisió estadística
Matemàtiques
Teoria matemàtica consistent en una aproximació unificadora a l’estadística matemàtica, basada en el concepte de joc d’estratègia, introduït per John von Neumann el 1928, que inclou l’estimació puntual i per intervals, com també la teoria dels contrasts d’hipòtesis.
La inicià el treball d’Abraham Wald Statistical Decisions Functions 1949 En la teoria de la decisió hom empra mostres aleatòries per tal de prendre decisions enfront d’incerteses respecte a diverses accions, entre les quals n'hi ha que poden ésser considerades millors que les restants Per exemple, en el cas d’un contrast paramètric d’hipòtesis, hom farà servir una mostra del collectiu, n'observarà una realització i, en vista de la valor presa per la funció de decisió, acceptarà o rebutjarà la hipòtesi En la teoria de la decisió, doncs, hom considera d’una banda un sistema probabilitzat o…
funció de risc
Matemàtiques
Funció que constitueix un dels elements essencials en la teoria de la decisió estadística i que representa l’esperança matemàtica de la pèrdua L.
Donat un espai de probabilitat H , A , M i una variable aleatòria x a valors en ℝ k i dependent d’un h ∈ H amb funció de densitat f h , hom considera les funcions de decisió d que a cada vector x 1 , , x n de valors de n variables independents amb la mateixa llei de x , associen una decisió Així mateix, la funció de pèrdua L h, d mesura la pèrdua produïda quan l’estat h és dut a terme i la decisió és presa La funció de risc és definida aleshores mitjançant la fórmula Hi ha altres possibles definicions, una mica més complicades Cal fer notar que en la funció de risc la informació donada…
mitjana
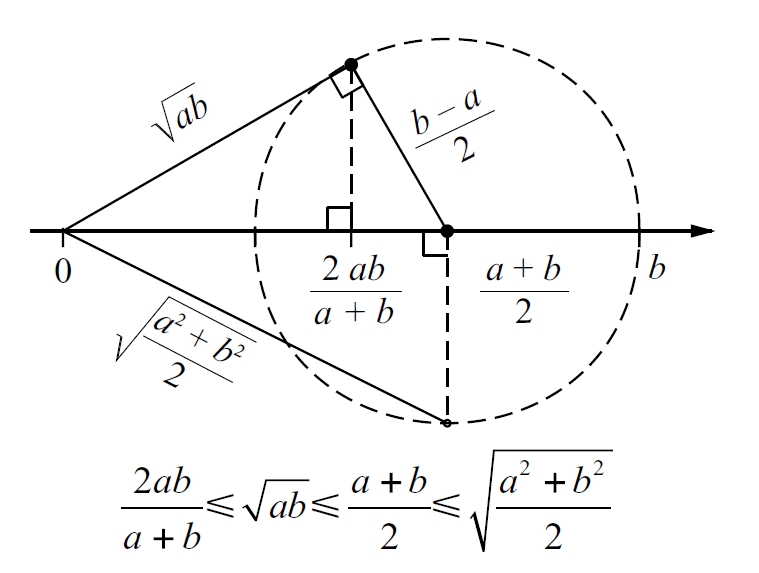
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
lema de Fatou-Lebesgue
Matemàtiques
Lema segons el qual l’esperança matemàtica de la variable aleatòria límit de la successió Xn és el límit de les esperances matemàtiques dels elements Xn.
Així, si X 1 , X 2 ,, X n és una successió de variables aleatòries i Y, Z són dues variables aleatòries, si X n ≤ Y per a tot n , aleshores i si X n ≥ Z per tot n , aleshores aleshores, si la successió X n és convergent i fitada, es compleix que