Resultats de la cerca
Es mostren 36 resultats
Pierre Petit
Física
Matemàtiques
Físic i matemàtic francès.
Fou alumne i amic de Descartes Ideà un aparell per a mesurar les distàncies estellars i una màquina de sumar cilíndrica estudià també els experiments baromètrics de Torricelli, que després exposà detalladament en diverses publicacions
teorema de Fermat
Matemàtiques
Teorema segons el qual si p és un nombre primer i a un nombre primer amb p, aleshores es satisfà que ap-1—1 és divisible per p, o sigui, ap-1≡(mod p).
La primera demostració d’aquest teorema fou feta per Euler el 1736
regle de càlcul

Regle de càlcul
(CC0)
Construcció i obres públiques
Matemàtiques
Petit instrument portàtil de fusta, metall, plàstic, etc. que permetia fer càlculs numèrics d’una manera ràpida i amb una certa aproximació raonable.
Consisteix en un regle proveït de diverses escales graduades, que duu, a més, un petit regle també graduat, desplaçable respecte al regle principal mitjançant unes ranures i uns encaixos adequats, i un cursor transparent, també desplaçable, proveït d’una o més ratlles verticals molt fines Totes les escales són logarítmiques, llevat d’alguna d’especial El principi en què es basa el regle de càlcul és la teoria dels logaritmes, de manera que per a multiplicar dos nombres, de fet hom suma dos segments graduats logarítmicament, i la divisió, anàlogament, consisteix a fer la…
fita inferior
Matemàtiques
En un conjunt de nombres, nombre igual o inferior al més petit de tots.
funció periòdica
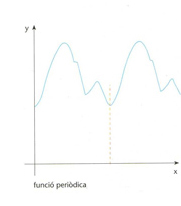
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
interval de confiança
Matemàtiques
Donat un paràmetre p a estimar, interval [p1, p2] tal que la probabilitat que el valor veritable de p hi pertanyi és igual a un valor prefixat 1-α.
Els valors p 1 i p 2 són els límits de confiança i 1-α és el nivell o grau de confiança de l’estimació L’estimació és tant més bona com més petit és l’interval de confiança i més gran el grau de confiança
límit d’una successió
Matemàtiques
Valor al qual una successió s’acosta més i més (tant com hom vulgui).
Donada una successió { a n }, a 1 ,, a n ,, hom diu que el límit de la successió és A , o que la successió tendeix a a , si per a tot real ε > 0, per petit que sigui, existeix un terme a m de la successió tal que si n > m aleshores | A-a n |