Resultats de la cerca
Es mostren 123 resultats
identificar
Matemàtiques
Reconèixer que dos objectes matemàtics, fins aleshores tractats diferentment, són el mateix.
reticle modular
Matemàtiques
Reticle (R, ∧, ∨) tal que si a<c aleshores a ∨(b ∧c) = (a ∨b) ∧c.
desigualtat de Bernoulli
Matemàtiques
Si dos membres reals, x i a, satisfan x>-1 i a>1, aleshores (1+x)a> 1+ax.
teorema d’Abel
Matemàtiques
Teorema segons el qual si una sèrie de potències convergeix per a x = c, aleshores convergeix absolutament per a |x | < |c|.
teorema de Brianchon
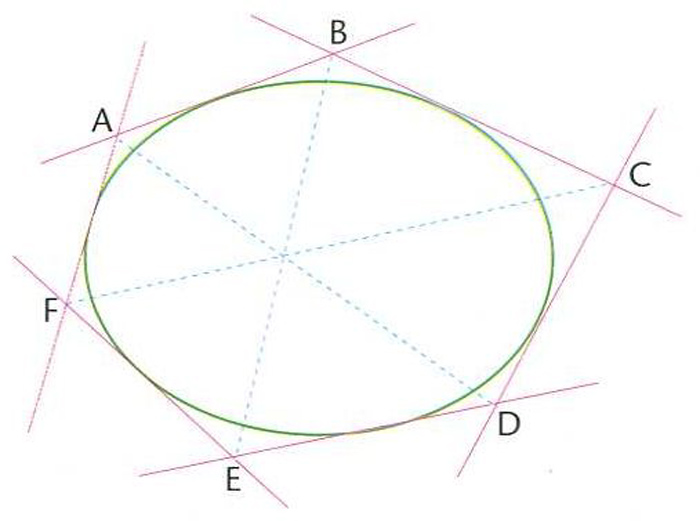
Teorema de Brianchon
© fototeca.cat
Matemàtiques
Teorema segons el qual si un hexàgon té els costats tangents a una cònica, aleshores tres de les seves diagonals són concurrents.
Un hexàgon d’aquest tipus s’anomena un hexàgon de Brianchon , i el punt de concurrència s’anomena punt de Brianchon Aquest teorema és el dual del teorema de Pascal
recobriment d’un conjunt
Matemàtiques
Família de subconjunts d’un conjunt donat tal, que la seva reunió conté el conjunt en qüestió, que és aleshores anomenat conjunt recobert
.
Les particions són un tipus particular de recobriment El recobriment és finit si és format per un nombre finit de subconjunts
lema de Fatou-Lebesgue
Matemàtiques
Lema segons el qual l’esperança matemàtica de la variable aleatòria límit de la successió Xn és el límit de les esperances matemàtiques dels elements Xn.
Així, si X 1 , X 2 ,, X n és una successió de variables aleatòries i Y, Z són dues variables aleatòries, si X n ≤ Y per a tot n , aleshores i si X n ≥ Z per tot n , aleshoresaleshores, si la successió X n és convergent i fitada, es compleix que
teorema de la invariància de dimensió de Brouwer
Matemàtiques
Teorema segons el qual si m ≠n, aleshores no hi ha cap homeomorfisme d’un obert de ℝm en un obert de ℝn.
matroide
Matemàtiques
Estructura algèbrica consistent en un conjunt E i un conjunt S de parts no buides de E que satisfan: tot singletó de E pertany a S
.
Si X ∈S , aleshores tota part Y no buida de E inclosa en X pertany també a S i, per a tota part A de E , si X i Y són dos elements de S continguts en A i maximals, aleshores card X = card Y La teoria de matroides fou introduïda per Withney el 1935 i ha experimentat un desenvolupament ràpid en ésser aplicada als espais vectorials i a la teoria de grafs
conjunt ordenat
Matemàtiques
Conjunt X
proveït d’una relació d’ordre ≤.
Si la relació d’ordre és parcial, el conjunt OOO X ,≤OOO és parcialment ordenat i, si és total, és totalment ordenat Una relació d’ordre és parcial si compleix les propietats reflexiva x ≤ x , transitiva si x ≤ y i y ≤ z , aleshores x ≤ z i antisimètrica si x ≤ y i y ≤ x , aleshores x = y I és total quan és parcial i, a més, tota parella d’elements és comparable qualssevol que siguin x , y , x ≤ y o y ≤ x
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina