Resultats de la cerca
Es mostren 14 resultats
homòleg | homòloga
Matemàtiques
Dit dels elements connectats per alguna relació, alguna correspondència o alguna transformació.
equació
Matemàtiques
Igualtat entre dues expressions matemàtiques que contenen alguna variable.
Si la igualtat no conté cap element variable, hom només pot dir que és certa o falsa si conté variables, la igualtat pot esdevenir certa per a uns valors i falsa per a uns altres en particular, pot ésser certa per a qualsevol valor de les variables anomenada aleshores identitat , o bé falsa per a qualsevol valor de les variables equació incompatible Els valors que satisfan una equació són les seves solucions o arrels En termes més generals, si en una correspondència entre dos conjunts numèrics o no hom fixa una imatge, la condició que determina quins elements originals tenen aquesta imatge…
sistema
Matemàtiques
Conjunt de quantitats o objectes que tenen alguna propietat comuna.
associatiu | associativa
Matemàtiques
Relatiu o pertanyent a alguna operació que té la propietat de l’associativitat.
teoria de les catàstrofes
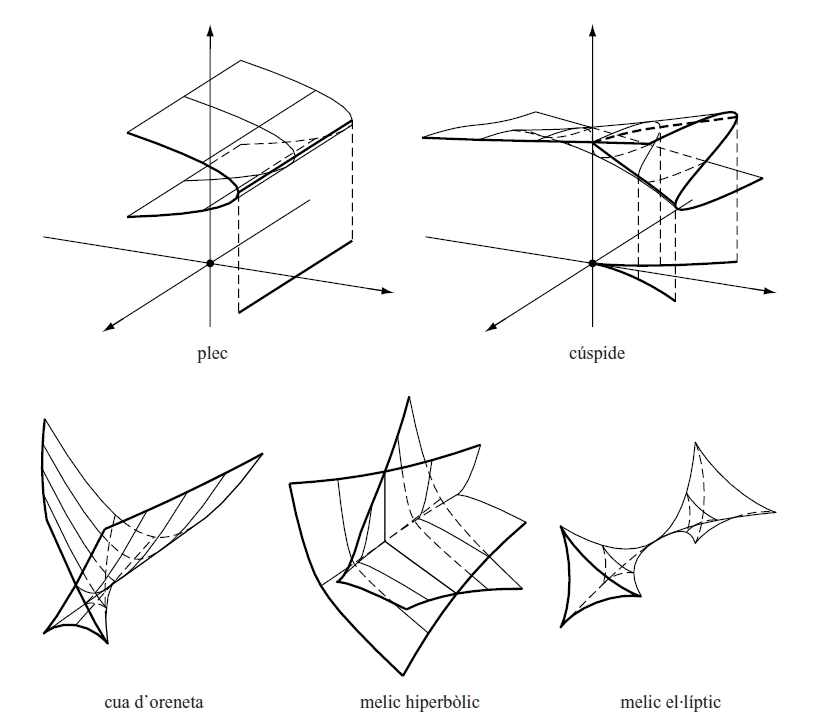
teoria de catàstrofes Les cinc catàstrofes elementals de codimensió menor que quatre
Física
Matemàtiques
Corpus teòric desenvolupat pel matemàtic francès René Thom d’ençà del 1972, i originat en l’intent de modelitzar els canvis discontinus que hom observa en la natura.
En molts sistemes, una petita variació quantitativa de les condicions inicials dóna lloc a una enorme diferència qualitativa en el comportament a llarg termini del sistema situació anomenada bifurcació de comportament Això és important per a l’estudi dels fenòmens d’estabilitat estructural, on cal que el sistema sigui insensible a petites pertorbacions En la teoria de les catàstrofes, aquest requeriment implica que el sistema dinàmic que modelitza el fenomen natural pugui ésser descrit localment per mitjà d’una de les set formes normals conegudes com a catàstrofes elementals , tot i que…
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A -1 La matriu…
regle de càlcul

Regle de càlcul
(CC0)
Construcció i obres públiques
Matemàtiques
Petit instrument portàtil de fusta, metall, plàstic, etc. que permetia fer càlculs numèrics d’una manera ràpida i amb una certa aproximació raonable.
Consisteix en un regle proveït de diverses escales graduades, que duu, a més, un petit regle també graduat, desplaçable respecte al regle principal mitjançant unes ranures i uns encaixos adequats, i un cursor transparent, també desplaçable, proveït d’una o més ratlles verticals molt fines Totes les escales són logarítmiques, llevat d’alguna d’especial El principi en què es basa el regle de càlcul és la teoria dels logaritmes, de manera que per a multiplicar dos nombres, de fet hom suma dos segments graduats logarítmicament, i la divisió, anàlogament, consisteix a fer la…
discontinuïtat
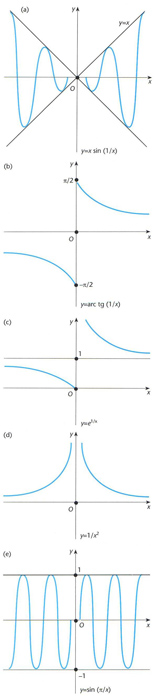
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi…
conjugat | conjugada
Matemàtiques
Dit de dues magnituds (punts, corbes, quantitats, estructures, operadors, etc) enllaçades per alguna llei o relació determinada (diàmetres conjugats d’una el·lipse, nombres complexos conjugats).