Resultats de la cerca
Es mostren 15 resultats
regla de tres
Matemàtiques
Algorisme utilitzat en la resolució de problemes de proporcionalitat.
En una funció de proporcionalitat directa y = kx , quan hom coneix x 1 , x 2 , y 1 = kx 1 i vol determinar y 2 , que es donat per la fórmula y 2 = y 1 / x 1 x 2 , aplica aquesta regla La regla de tres consisteix a collocar les dades en la forma x 1 - y 1 x 2 - y 2 i aplicar que y 2 = x 2 y 1 / x 1 Aquesta és la regla de tres simple directa Però quan en una funció de proporcionalitat inversa y = k/x , hom coneix x 1 , x 2 , y 1 = k/x 1 , i vol determinar y 2 = k/x 2 , que resulta de y 2 = y 1 x 1 / x 2 , la regla de tres consisteix aleshores a disposar les dades com abans x…
loxodromia
Matemàtiques
En una superfície de revolució, corba de la superfície que forma amb les generatrius un angle constant.
Tenen una especial importància les loxodromies d’una superfície esfèrica, perquè permeten d’aplicar aquest concepte a la superfície de la Terra
Antoni Alà
Economia
Matemàtiques
Primer director de l’Escola de Càlcul Teoricopràctic establerta per la Junta de Comerç barcelonina el 1815.
És autor d’una memòria sobre geometria i d’altres treballs, i anà a Madrid a estudiar el nou sistema de comptabilitat per partida doble per aplicar-lo a Barcelona
Giovanni Alfonso Borelli
Matemàtiques
Matemàtic i metge italià, condeixeble de Torricelli, professor de matemàtiques a Messina i a Pisa.
Ultra fer investigacions en els camps de la física i de l’astronomia i ésser el creador, en medicina, de l’escola iatromecànica, en la seva obra fonamental De motu animalium 1680-81, fruit de mig segle de treballs, intentà per primera vegada d’aplicar mètodes matemàtics a l’estudi dels problemes de la mecànica del moviment dels animals
ergodicitat
Matemàtiques
Propietat d’un procés estocàstic en què tots els paràmetres probabilístics es poden determinar (amb probabilitat 1) d’una única funció qualsevol resultant del procés.
Aquesta propietat normalment s’expressa, també, dient que les mitjanes probabilístiques coincideixen amb les temporals En sentit ampli hom parla d’ergodicitat respecte a la mitjana, desviació típica o qualsevol altre paràmetre d’interès Els processos ergòdics són importants en el sentit que hom pot fer fàcilment mesures sobre una única funció resultant d’un fenomen físic, i aplicar els valors resultants a la teoria matemàtica dels processos estocàstics
Adolphe Quételet
Matemàtiques
Sociologia
Estadístic, matemàtic i sociòleg belga.
Professor a Gant i a Brusselles, dirigí la construcció de l’observatori de Brusselles i en fou el primer director 1828 Aplicà la teoria de les probabilitats a les ciències socials i a l’antropometria i constatà la regularitat en fenòmens on hom creia que es reflectia el lliure albir Observà, a més, que aquesta regularitat s’ajusta a una corba de distribució d’aquí sortí el concepte d’home mitjà, central en la seva teoria Fou també el primer a aplicar l’estadística als fenòmens socials, base de la sociologia i del neopositivisme actual Aplicà les seves recerques a observacions d’…
semblança
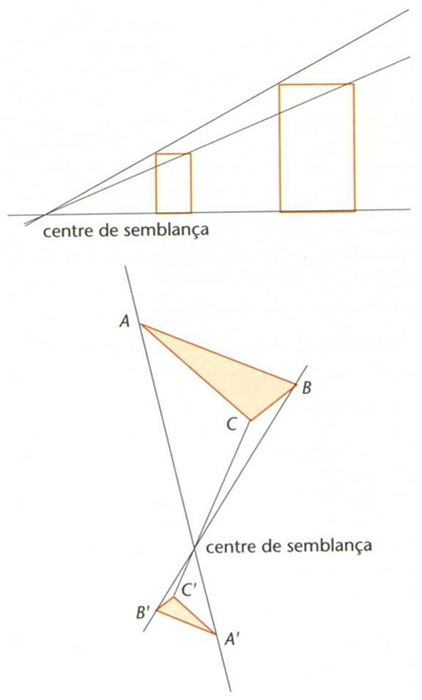
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament…
transformació
Matemàtiques
Aplicació bijectiva d’un conjunt en un altre o en ell mateix.
El conjunt de les transformacions d’un conjunt en ell mateix té estructura de grup respecte a la composició de transformacions la composició en el sentit d’aplicar successivament de manera ordenada dues transformacions és anomenada també producte Segons la definició de Felix Klein, la geometria és l’estudi de les nocions invariants per a un grup de transformacions geometria Com a exemples de transformacions en el pla poden ésser esmentades les rotacions, les simetries axials, les translacions, etc i en l’espai, les simetries respecte a un eix o a un pla, les rotacions axials,…
addició
Matemàtiques
Operació consistent a fer correspondre a cada parell d’elements d’un determinat conjunt un altre element del mateix conjunt, anomenat suma.
La definició específica d’addició varia segons els elements als quals hom la vulgui aplicar Entre nombres naturals, el resultat de l’addició, és a dir, la suma, és el nombre natural que representa el conjunt que és reunió de dos conjunts sense elements comuns que representin els addends Si A té dos elements, A = {a,b}, i B té tres elements, B = {c,d,e}, la reunió A∪B = {a,b,c,d,e} té cinc elements, 2 + 3 = 5 Entre nombres reals, el resultat de l’addició és obtingut sumant o restant els valors absoluts dels addends segons que aquests siguin del mateix signe o de signe contrari El…
funció de distribució
Matemàtiques
Funció associada a una variable aleatòria que dona les probabilitats que aquesta prengui uns certs valors determinats.
Per a cada nombre real x , la funció de distribució F X pren el valor F X x = P {ϖ| X ϖ ≤ x } = P X ≤ x format per tots els esdeveniments elementals tals que el valor X ϖ no ultrapassa x Les propietats més importants que compleix la funció de distribució són si X és una variable aleatòria i F X la seva funció de distribució, sempre que x 1 < x 2 hom tindrà que F X x 1 ≤ F X x 2 si F X és una funció de distribució d’una variable aleatòria X , i si F X és la funció de distribució d’una variable aleatòria X , Les principals funcions de distribució són la distribució binomial ,…