Resultats de la cerca
Es mostren 30 resultats
aproximació
Matemàtiques
Ordre de grandor de les desviacions que els valors mesurats o calculats d’una magnitud en un sistema presenten respecte al valor teòric que compliria amb exactitud la llei matemàtica que determina aquest sistema.
El comportament de qualsevol sistema és determinat per unes lleis que es tradueixen en relacions matemàtiques entre les magnituds que defineixen Per exemple, pel corrent elèctric val la llei d’Ohm V = R × I , on V és la tensió aplicada, R la resistència del cos considerat i I la intensitat del corrent en aquestes condicions La validesa d’aquestes lleis significa que, si hom fa mesures independents de cadascuna de les quantitats que hi intervenen V, R i I en l’exemple, els valors obtinguts han de mantenir entre ells la relació matemàtica que expressa la llei del sistema aquest fet, però, no…
càlcul numèric
Matemàtiques
Sèrie de mètodes que permet d’obtenir aproximació de les solucions d’un problema matemàtic.
El concepte d’aproximació resta determinat per la natura del conjunt o espai sobre el qual hom calcula i, alhora, per la mètrica o distància definida en ell Donat un espai funcional on hi ha definida una mètrica, aquesta permet de definir una topologia, la qual, a la vegada, ens dóna el concepte de proximitat Un cop fixat l’espai on hom opera i la mètrica que ens definirà la noció d’aproximació, el procés del càlcul numèric es resumeix de la manera següent recull de les dades inicials I del problema dades d’entrada, determinació d’un algorisme de càlcul A , i obtenció de resultats R Aquest…
aritmètica finita
Matemàtiques
Estudi de les aproximacions dels nombres reals, mitjançant nombres racionals amb un nombre determinat de decimals, i de les operacions d’addició, subtracció, multiplicació, divisió, potenciació, extracció d’arrels, etc.
Cal controlar la manera amb què s’aproxima procés d’aproximació l’error en fer l’aproximació i, finalment, la propagació de l’error control i anàlisi de l’error
definició
Matemàtiques
Introducció d’un nou concepte fent referència a conceptes anteriors ja definits.
Necessàriament hi ha, doncs, conceptes primaris o no definibles, reduïts, en primera aproximació, als conceptes de conjunt, element, i pertinença Hom axiomatitza aquests conceptes primaris per tal d’evitar contradiccions aquest procés constituiex l’objecte de la teoria de conjunts conjunt
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una aproximació polinòmica a la funció f x amb la fórmula d’interpolació de Newton en la qual, si f x és n vegades…
fórmula del trapezi
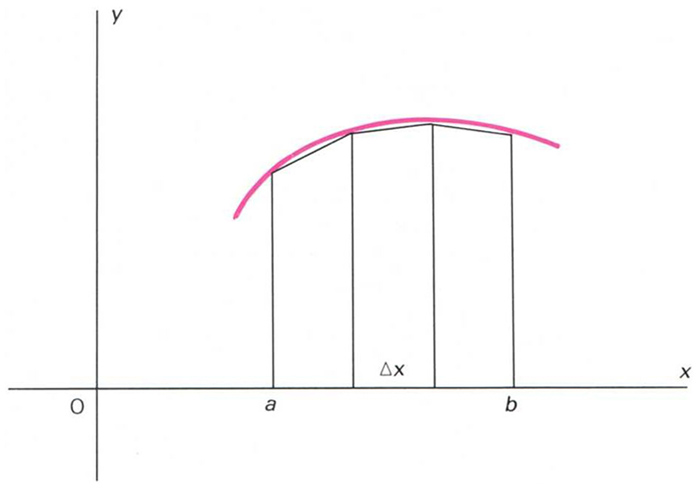
Aplicació de la fòrmula del trapezi
© fototeca.cat
Matemàtiques
Regla utilitzada per a aproximar l’àrea compresa entre una corba, una línia horitzontal i dues de verticals que tallen la corba.
Hom divideix el segment horitzontal en diverses parts iguals i dibuixa les perpendiculars des de cada punt de divisió a la corba després les interseccions d’aquestes rectes amb la corba són unides mitjançant línies rectes, successivament La suma de les àrees dels trapezis així engendrats representa una aproximació de l’àrea limitada per la corba
llei de Student
Matemàtiques
Llei, coneguda també com a llei t de Student, introduïda per W. S. Gossett, que correspon a la funció de distribució següent: .
El paràmetre n és anomenat graus de llibertat de la llei Quan n tendeix a infinit, aquesta distribució tendeix a una distribució normal , però, de fet, per a n major de 30 la llei normal ja és una bona aproximació Això fa que aquesta llei sigui emprada com a prova d’hipòtesi per a analitzar si una distribució és normal o no
Ars conjectandi
Matemàtiques
Obra pòstuma de Jakob Bernoulli publicada a Basilea el 1713.
Conté una reedició comentada de l’obra de jocs d’atzar de Christiaan Huygens De ratiociniis in ludo ale 1617 Enuncia el teorema que porta el seu nom, segons el qual, augmentant suficientment el nombre d’observacions, hom pot aconseguir qualsevol aproximació prefixada Aquesta obra, preludi del teorema dels grans nombres de Čebyšov, fou una aportació importantíssima a la teoria de la probabilitat
interpolació
Matemàtiques
Procediment que, donats els n valors y 1, y 2, ..., yi, ..., yn d’una funció y = g(x) en els punts x 1, x 2..., xi, ..., xn, permet de calcular, aproximadament, els valors de g(x) en punts intermedis als donats.
Més exactament, la interpolació consisteix a trobar una altra funció y = f x , d’un tipus escollit, que passi pels punts x i , y i Una primera aproximació és constituïda per la interpolació lineal , que consisteix a imposar que, entre cada dos punts consecutius dels donats, f x sigui un segment de recta En la interpolació de Lagrange , f x és un polinomi de grau n- 1 donat per la fórmula Si els punts x i constitueixen una progressió aritmètica, és emprada la interpolació de Newton càlcul de diferències diferència
teorema central del límit
Matemàtiques
Teorema segons el qual, per a una distribució de probabilitat arbitrària de mitjana μ i variància σ2, i essent x̄ la mitjana de n observacions independents d’aquesta distribució, la variable
té una distribució
.
Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/ n de la d’aquesta A la pràctica, per a n ≥ 10 l’aproximació és ja suficient Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries Això explica per què a la pràctica hi ha moltes variables que segueixen una…