Resultats de la cerca
Es mostren 7 resultats
anàlisi harmònica
Matemàtiques
Representació de funcions periòdiques mitjançant sumació i integració de desenvolupaments en sèrie d’algunes funcions trigonomètriques elementals.
Permet d’obtenir expressions senzilles aproximades de les funcions i deduir propietats generals a partir de les propietats particulars d’aquelles funcions elementals
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per defecte i per…
àlgebra no commutativa
Matemàtiques
Part de l’àlgebra, entesa com a teoria de les estructures algèbriques, que estudia precisament aquelles estructures algèbriques en les quals l’operació fonamental no és pas commutativa.
Principalment es preocupa de la teoria de grups
mesura
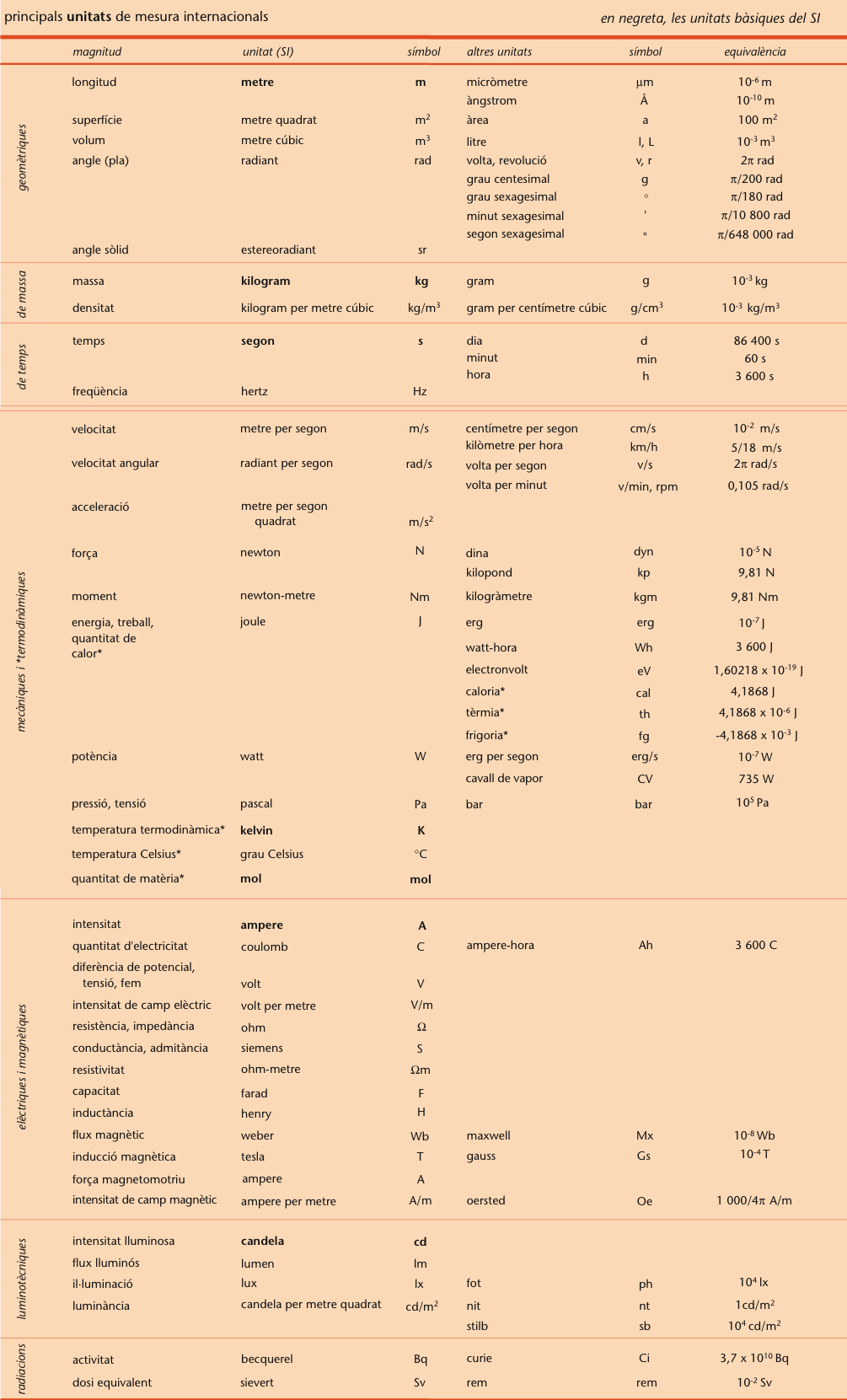
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són mesurables en un…
Josep Vicent de l’Olmo i Conca
Literatura catalana
Matemàtiques
Arqueologia
Història
Generós i secretari del Tribunal del Sant Ofici de la Inquisició de la seva ciutat natal, s’interessà per la matemàtica i per la poesia.
Succeí el seu pare com a secretari del tribunal de la inquisició de València La seva fama d’home assenyat el convertí en conseller polític de la ciutat —el 1661 formà part del consell general—, segons informen alguns dels seus contemporanis Formà part d’acadèmies de matemàtiques —fou membre de l’acadèmia de l’Alcàsser i el 1685 de la que presidia el comte d’Alcúdia Onofre Vicent Escrivà d’Íxer, on parlà diverses vegades sobre l’esfera— i com a poeta també participà en diversos certàmens religiosos Guanyà el primer premi de poesia als certàmens dels anys 1665, 1667 i 1668, sempre amb…
, ,
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema si aquestes…