Resultats de la cerca
Es mostren 240 resultats
mètode dels mínims quadrats
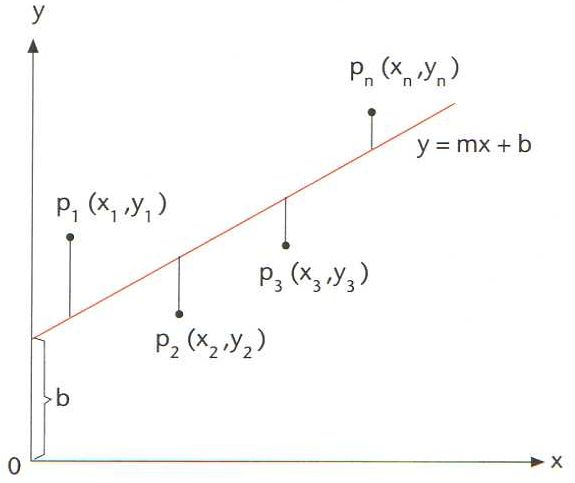
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat…
producte mixt
Matemàtiques
Donats tres vectors, a, b i c, nombre (a, b, c) donat per (a, b, c) = a·(b ∧c), on el signe ∧indica el producte vectorial.
Geomètricament representa el volum del parallelepípede determinat pels vectors a, b i c
correspondència
Matemàtiques
Una correspondència entre dos conjunts A
i B
és definida com un subconjunt del producte cartesià A × B
.
És fàcil de relacionar aquesta definició amb la idea intuïtiva de correspondència per exemple, si A és el conjunt dels països, i B el dels idiomes, la correspondència tal idioma es parla a tal país determina exactament un subconjunt de A × B el de les parelles a, b tals, que en el país a es parla l’idioma b En una correspondència el conjunt d’elements de A que apareixen com a primers elements de parelles de la correspondència és anomenat domini , i el conjunt d’elements de B que apareixen com a segons elements en les parelles de la correspondència, imatge Si cada element del domini només…
interval
Matemàtiques
Donats dos nombres reals a i b, anomenats extrems, conjunt de nombres reals compresos entre a i b
.
Quan el conjunt no inclou els extrems, l’interval és anomenat obert , i hom el representa per a,b o per a,b altrament, l’interval és anomenat tancat , i hom el representa pel símbol a, b En el cas que l’interval inclogui només un dels extrems, és anomenat semiobert , i hom el representa per a,b o per a,b , si és a el punt inclòs en l’interval
subtracció
Matemàtiques
Donats dos nombres a
i b
, operació consistent a determinar el nombre c
tal, que c
+ b
= a
.
El nombre a és el minuend , i b el subtrahend c és la resta o residu En un grup additiu qualsevol, la resta '' a menys b ' és el resultat de sumar a a l’element oposat del b , i això és indicat per c = a - b
esfera
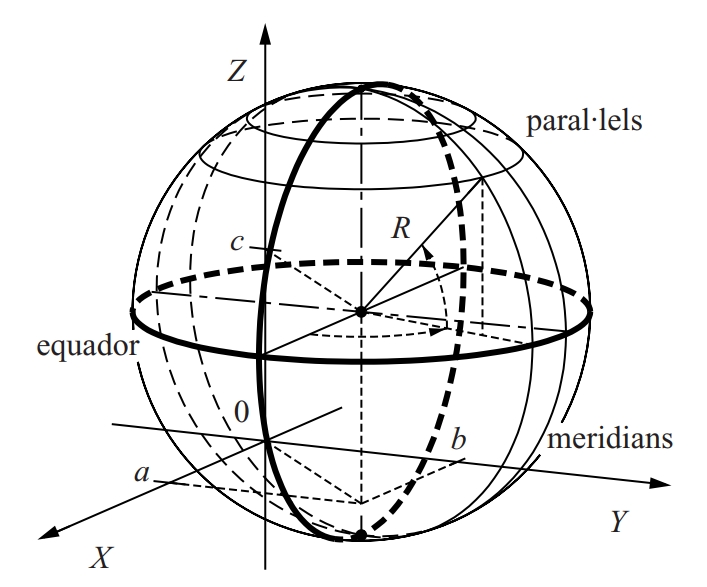
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
gràfic | gràfica
Matemàtiques
Subconjunt del producte cartesià A × B de dos subconjunts; es tracta doncs, d’una colla de parelles d’elements (a, b), on a ∈A i b ∈B.
En el cas que A i B siguin, respectivament, el domini de definició i la imatge d’una funció, el gràfic corresponent és anomenat també gràfica funcional o corba associada a la funció
multiplicació
Matemàtiques
Operació aritmètica que, donats dos nombres naturals a (el multiplicand) i b (el multiplicador), consisteix a trobar un nombre, ab, a × b o a · b, que és el resultat de sumar b vegades el nombre a
.
En teoria de conjunts, hom defineix el nombre ab com el cardinal del producte cartesià A × B , on A és un conjunt de cardinal a , i B un conjunt de cardinal b La multiplicació és anomenada també producte i gaudeix de les propietats associativa, commutativa i distributiva respecte a la suma En les successives extensions del conjunt de nombres naturals fins a arribar als nombres complexos, hom va generalitzant convenientment la definició de la multiplicació, sense perdre, però, cap de les propietats anteriors ni tampoc la propietat que l’element neutre es…
ultramètrica
Matemàtiques
Aplicació d d’un conjunt A X A = {(a, b) | a ∈A, b ∈A} en la recta real, ℝ+, positiva.
L’aplicació és simètrica d a, b = d a, b , és separadora d a,b = 0 si i només si a Y b i compleix una desigualtat triangular generalitzada donats tres punts, a, b, c, la d a,b és menor que el màxim de d a,c i d c,b Tota ultramètrica és una distància o mètrica distància 4
biquaternió
Matemàtiques
Nombre hipercomplex de forma A + i B, essent A i B quaternions.
Aquesta noció és deguda a Hamilton 1895 i cal distingir-la de la donada per Cayley 1873 consistent en nombres de la forma A + wB , amb A i B quaternions reals, w un element que commuta amb els nombres reals i tal que w 2 = 1
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina