Resultats de la cerca
Es mostren 12 resultats
funció homogràfica
Matemàtiques
Funció f:ℂ→ℂdefinida per f(z)=(az+b)/(cz+d) quan z≠∞ i z≠-d/c, i per f(∞)=a/c i f(-d/c)=∞.
Quan ad - bc ≠0 hom parla de funció homogràfica pròpia , i quan ad - bc =0 de funció homogràfica impròpia
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el producte , per a, b c, d = ac + bd, ad + …
nombre racional
Matemàtiques
Conjunt de fraccions equivalents que representen una mateixa quantitat, entera o no.
Dues fraccions a / b , c / d són equivalents o iguals si, i només si, els parells de nombres enters que les constitueixen compleixen la relació ad = bc Cada classe de fraccions equivalents en aquesta relació d’equivalència és un nombre racional Si la fracció que defineix un nombre racional té numerador múltiple del denominador, és a dir, a = kb k ∈ℤ, la fracció a / b és equivalent a k/ 1, que hom acostuma a escriure en la forma k/ 1 = k En aquest sentit hom pot dir que els nombres enters són un subconjunt dels racionals Entre els nombres racionals hom pot definir les…
modular
Matemàtiques
Dit del grup de transformacions del pla complex del tipus w = (az+b)/ (cz+d), essent a, b, c i d nombres enters que compleixen la condició ad-bc = +1.
Tota transformació d’aquest grup transforma el semiplà complex superior en ell mateix i deixa invariant l’eix real Aquest grup és utilitzat per a definir la funció modular J , que té un paper fonamental en l’estudi de les funcions ellíptiques
teorema de Menelau
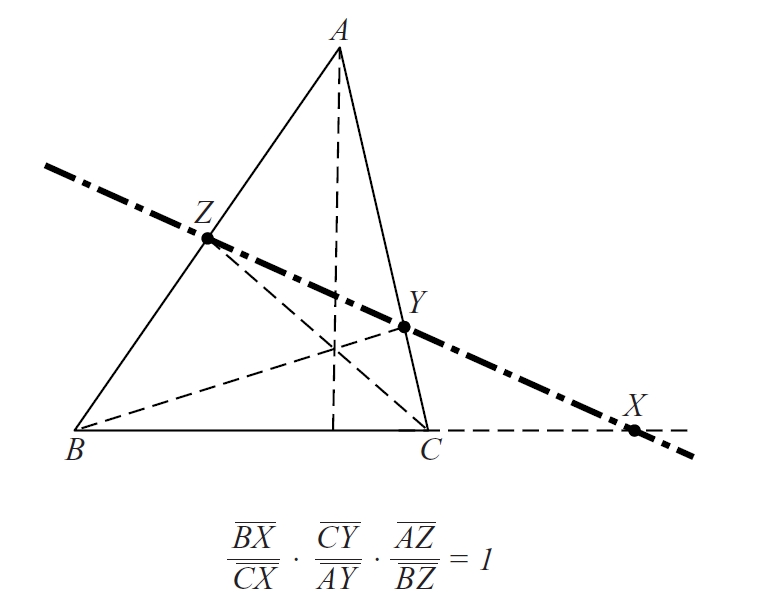
teorema de Menelau
© fototeca.cat
Matemàtiques
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
divisió harmònica
Matemàtiques
Conjunt de dues parel·les de punts A,B i C,D d’una mateixa recta tals, que els dos punts d’una mateixa parel·la divideixen el segment format pels dos altres punts en les raons oposades AC/AD = BC/BD.
Cada punt d’aquesta divisió és anomenat conjugat harmònic del seu associat respecte als altres dos
divisibilitat
Matemàtiques
Conjunt de condicions que han de complir dos nombres enters per tal que hom pugui efectuar la divisió exacta de l’un per l’altre, o sia, que compleixin la condició a = bc, a essent el múltiple, b, el divisor, i c, el quocient exacte.
Per efectuar aquest estudi hom parteix de la descomposició en factors primers a ℤ Les proves de divisibilitat permeten de saber si un nombre és divisible per un altre sense necessitat de fer-ne la divisió En són exemples els següents tot nombre acabat en un dígit parell és divisible per 2 tot nombre acabat en 0 o 5 és divisible per 5 tot nombre tal que la suma dels seus dígits és 3 o 9 és divisible, respectivament, per 3 o 9 si els dos darrers dígits d’un nombre formen un nombre divisible per 4, el nombre original també ho és i qualsevol nombre la suma dels dígits del qual és divisible per 3…
domini d’integritat
Matemàtiques
Anell commutatiu amb unitat i sense divisors de zero o, altrament, on val la llei de simplificació (si a, b són dos elements qualssevol de A i c és un tercer element de A diferent de zero, ac = bc si i només si a = b)
.
teorema de Desargues
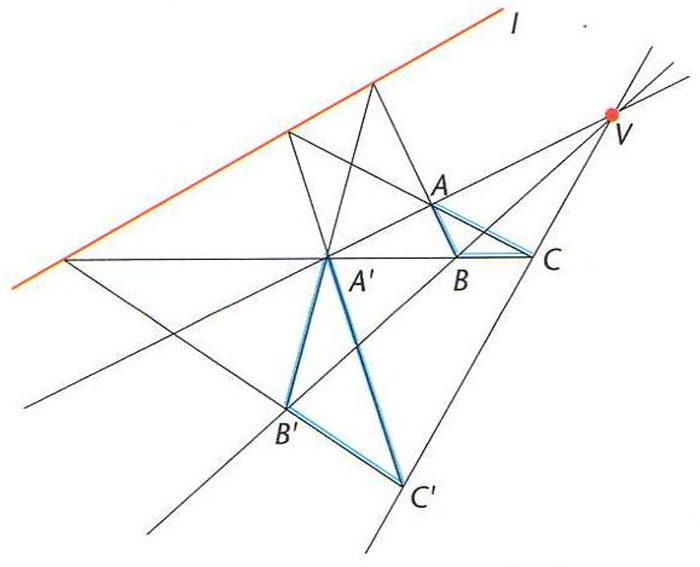
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.
teorema de Ceva
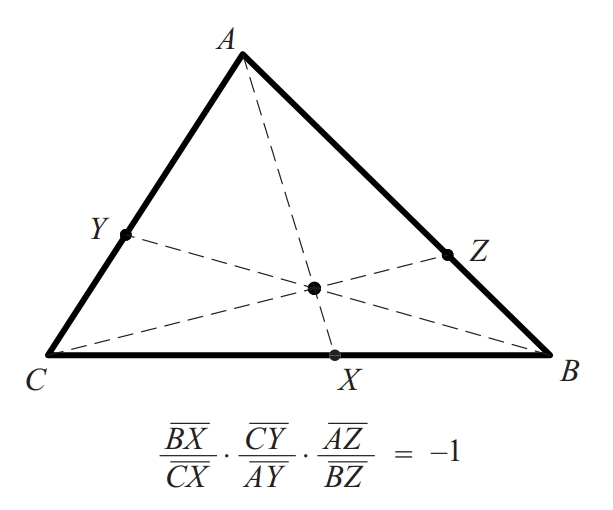
teorema de Ceva
Matemàtiques
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau