Resultats de la cerca
Es mostren 27 resultats
producte cartesià de dos conjunts
Matemàtiques
Donats dos conjunts, A i B, conjunt A x B format per totes les parelles ordenades (a, b) en què a ∈A i b ∈B
.
multiplicació
Matemàtiques
Operació aritmètica que, donats dos nombres naturals a (el multiplicand) i b (el multiplicador), consisteix a trobar un nombre, ab, a × b o a · b, que és el resultat de sumar b vegades el nombre a
.
En teoria de conjunts, hom defineix el nombre ab com el cardinal del producte cartesià A × B , on A és un conjunt de cardinal a , i B un conjunt de cardinal b La multiplicació és anomenada també producte i gaudeix de les propietats associativa, commutativa i distributiva respecte a la suma En les successives extensions del conjunt de nombres naturals fins a arribar als nombres complexos, hom va generalitzant convenientment la definició de la multiplicació, sense perdre, però, cap de les propietats anteriors ni tampoc la propietat que l’element neutre es pot anar identificant…
Pierre Gassendi
Filosofia
Física
Matemàtiques
Cristianisme
Clergue; matemàtic, físic i filòsof materialista francès.
Estudià teologia, grec i hebreu a Ais de Provença i es doctorà en teologia a Avinyó Fou professor 1645 al Collège Royal de París És conegut pels seus atacs a la filosofia dels aristotèlics, que considera com a purament verbal, car, per a ell, la veritable ciència ha de partir de les qualitats experimentals de les coses Fonamenta el coneixement en una doctrina sensualista i en l’atomisme clàssic de Demòcrit i Epicur Fou amic de Hobbes, entusiasta de Galileu, Copèrnic i Kepler i contradictor de l’intellectualisme cartesià Escriví llibres de física, matemàtiques, astronomia i…
nombre complex
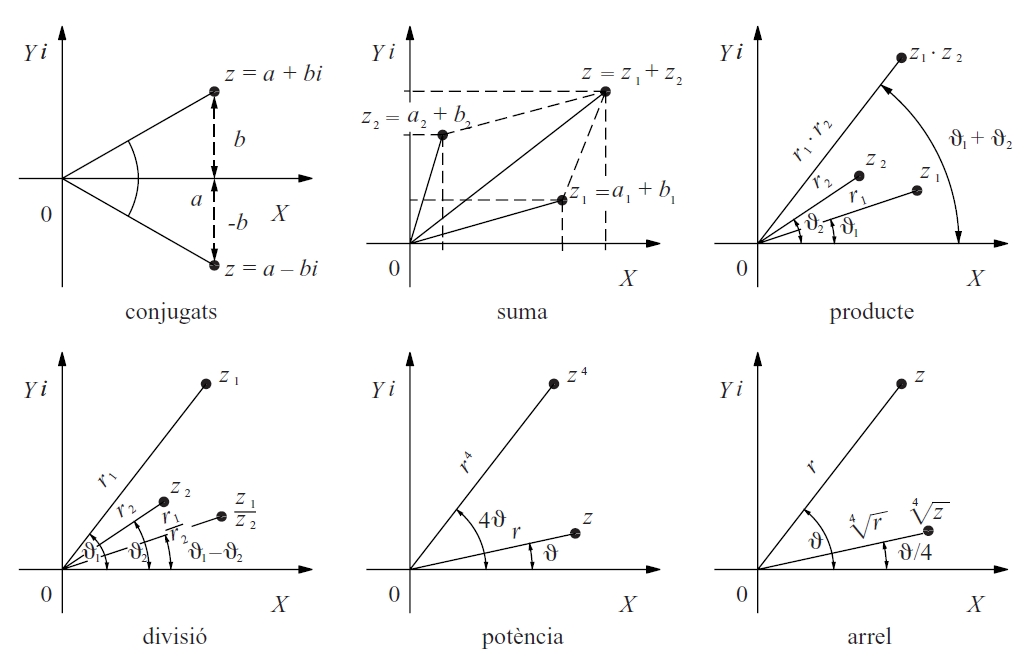
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
Ruggero Giuseppe Boscovich
Astronomia
Física
Matemàtiques
Físic, astrònom i matemàtic italià, d’origen croat.
Cursà estudis de física i matemàtiques al Collegium Romanum, i el 1726 entrà a la Companyia de Jesús En collaboració amb Christopher Mainer amidà l’arc de meridià entre Roma i Rímini 1750-53 En ésser els jesuïtes expulsats d’Itàlia el 1773, anà a París per invitació de Lluís XIV, on li fou concedida la direcció del departament d’òptica naval fins el 1782, que tornà a Itàlia A la seva obra fonamental, Theoria philosophiae naturalis redacta ad unicam legem virium in natura existentium Viena, 1758, criticà els conceptes fonamentals de l’obra de Newton, considerant-los similars als suscitats per…
uniformitat
Matemàtiques
Família F de subconjunts d’un producte cartesià T × T
.
Compleix x,x pertany a qualsevol element de F , per a tot x si V és de F, V - 1 = { x,y | y,x és de V} és també de F i per a tot V de F existeix un altre W tal que WW = { x,z | existeix y en T i x,y ∈ W , y,z ∈ W} és un subconjunt de V Tota uniformitat dóna lloc a un espai topològic i aquest és metritzable la seva topologia prové d’una distància si és de Hausdorff i la uniformitat té una base numerable Per exemple, si T és un espai mètric, amb distància d , el conjunt de subconjunts de T × T , U ∈ = { x,y | d x,y πε} és una uniformitat La parella T,F , on T és conjunt i F…
parella
Matemàtiques
Cadascun dels elements d’un producte cartesià de dos conjunts.
triplet
Matemàtiques
Cadascun dels elements d’un producte cartesià de tres conjunts.
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols…
operació
Matemàtiques
Aplicació del producte cartesià de dos conjunts en un altre conjunt.
Les operacions en què tots tres conjunts són el mateix conjunt, com en les quatre regles aritmètiques, són anomenades operacions internes Les operacions en què el segon i el tercer conjunts són iguals, com en la multiplicació d’un vector per un escalar, són anomenades operacions externes