Resultats de la cerca
Es mostren 39 resultats
nombre complex
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
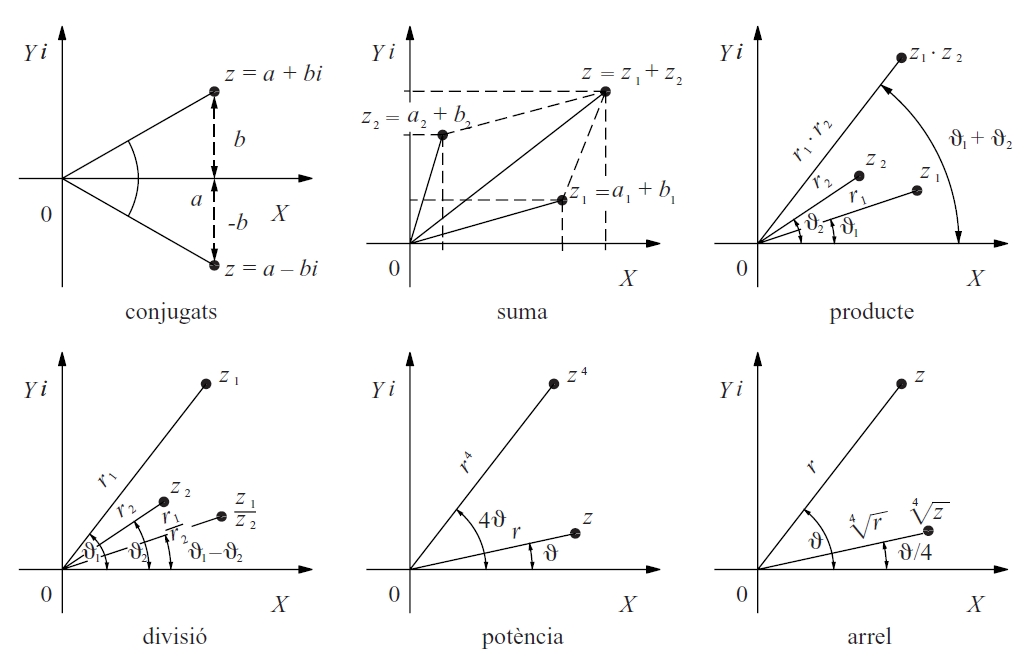
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
funció complexa
Matemàtiques
Funció el recorregut de la qual és un subconjunt del cos dels nombres complexos.
És anomenada també funció de valors complexos
teorema fonamental de l’àlgebra
Matemàtiques
Tota equació polinòmica de grau n>0 amb coeficients complexos té almenys una arrel complexa
.
Com a conseqüència, tot polinomi de grau n > 0 amb coeficients complexos pot descomposar-se en producte de n factors lineals La primera demostració rigurosa fou atribuïda a Gauss
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
associativitat
Matemàtiques
Propietat que tenen moltes operacions matemàtiques binàries d’acord amb la qual per a fer l’operació de tres elements es poden operar els dos primers i després operar el resultat amb el tercer element o bé operar el primera amb l’operació dels dos darrers.
La suma i la multiplicació dels nombres reals o complexos presenten aquesta propietat
rampa
Electrònica i informàtica
Matemàtiques
Funció que creix linealment amb el temps des de zero fins a un valor determinat, d’acord per tant amb l’expressió f(t) = kt
.
És una funció emprada sobretot en anàlisi transitòria de circuits elèctrics i sistemes complexos
nombres conjugats
Matemàtiques
Dit de dos nombres algèbrics sobre un camp donat si són arrels de la mateixa equació irreductible amb coeficients en el camp.
Així, els nombres complexos a + bi, a-bi són conjugats sobre el camp real, puix que són arrels de l’equació X 2 - 2aX + a 2 + b 2 = 0
quaternió
Matemàtiques
Símbol del tipus a +bi + cj +dk, on a, b, c, d són nombres reals i i, j, k segueixen les regles formals algèbriques: i2 = j2 = k2 = -1, i · j =-j · i =k, j k = -k . j = i, k . i =-i · k = j
.
Els quaternions poden ésser operats algèbricament suma i producte, com els complexos, dels quals són una extensió El conjunt dels quaternions té estructura de cos no commutatiu Els quaternions foren introduïts i estudiats per WRHamilton
funció gamma
Matemàtiques
Funció definida per la fórmula, deguda a Euler, Γ( x
) = ∫
t ( x - 1 )
e - t
, on, si hom considera Γ real, x
ha d’ésser real i major que zero, i si hom considera Γ complexa, la part real de x
ha d’ésser major que zer¦.
Segons Gauss, hom pot definir també la funció Γ amb l’expressió on x pot ésser qualsevol nombre real o complex, excepte enter negatiu Les propietats immediates de la funció Γ són Γ x +1 = x Γ x Γ1 = 1 Γ n = n-1 , per a n natural Una aplicació important de la funció Γ és que permet de generalitzar el concepte de factorial a nombres reals no enters i a nombres complexos