Resultats de la cerca
Es mostren 5 resultats
cub
Matemàtiques
Políedre regular format per sis cares quadrades.
Les tres arestes concurrents a cada vèrtex són perpendiculars entre elles en conseqüència, el tríedre format per les tres arestes és trirectangle, els díedres definits per dues cares amb una aresta comuna són rectes, i les cares oposades són paralleles Les quatre diagonals del cub es tallen en un punt, el centre del cub, que és, alhora, el centre de simetria d’aquesta figura Si la longitud de l’aresta del cub és a , el volum del cub val a 3 , i la seva diagonal té una longitud de a √3
teorema de Tales
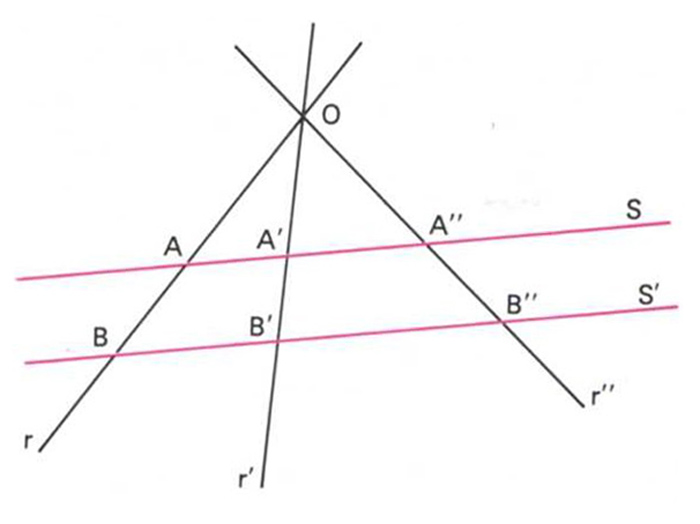
Teorema de Tales
© fototeca.cat
Matemàtiques
Teorema que estableix la proporcionalitat dels segments interceptats per rectes paral·leles sobre un feix de rectes concurrents.
Així, si tres rectes r, r´ i r’ que es tallen en O, són interceptades per les rectes paralleles en S, i en els punts B, B´ i B’ en S´, el teorema de Tales permet d’establir, entre d’altres, les següents relacions
teorema de Brianchon
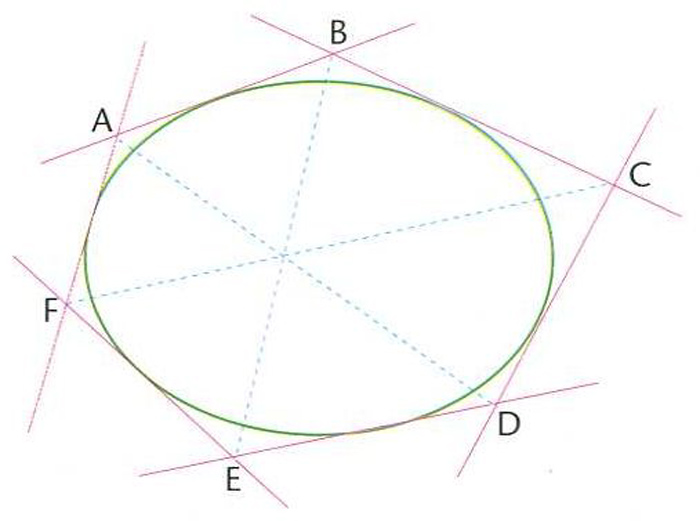
Teorema de Brianchon
© fototeca.cat
Matemàtiques
Teorema segons el qual si un hexàgon té els costats tangents a una cònica, aleshores tres de les seves diagonals són concurrents.
Un hexàgon d’aquest tipus s’anomena un hexàgon de Brianchon , i el punt de concurrència s’anomena punt de Brianchon Aquest teorema és el dual del teorema de Pascal
teorema de Desargues
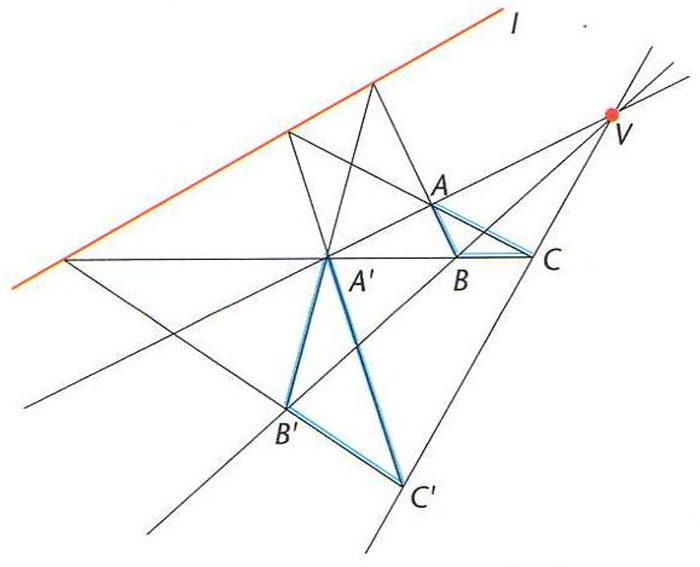
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.
teorema de Ceva
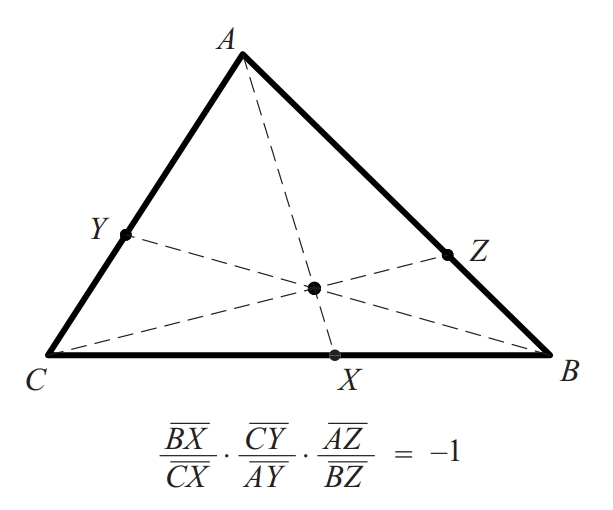
teorema de Ceva
Matemàtiques
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau