Resultats de la cerca
Es mostren 9 resultats
teorema de Gödel
Lògica
Matemàtiques
Teorema segons el qual, si una teoria T és no contradictòria i si els axiomes de l’aritmètica són teoremes de T, aleshores T no és categòrica (dit d’una altra manera, existeixen relacions indeterminables en T).
D’aquí es desprèn que una teoria que contingui l’aritmètica és no contradictòria
paraboloide hiperbòlic
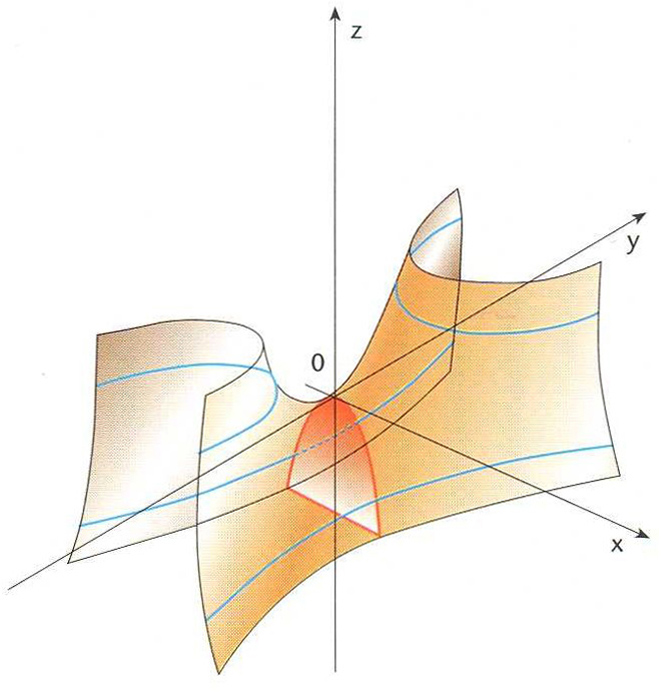
Paraboloide hiperbòlic on hi ha traçada una paràbola i dues hipèrboles
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
—
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola i la intersecció amb un pla perpendicular a l’anterior és una hipèrbola
paraboloide el·líptic
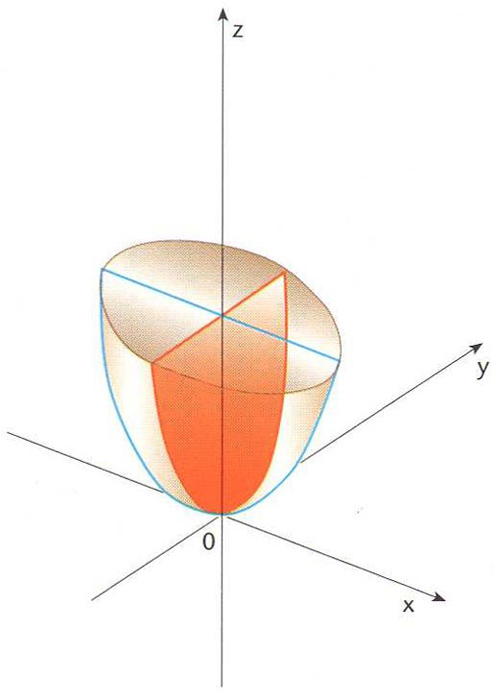
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse
superfície desenvolupable
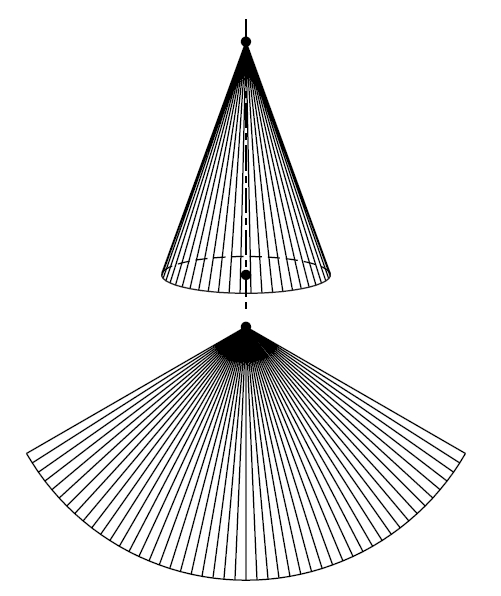
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
cos complex
Matemàtiques
L’equació quadràtica x2 + 1 = 0 no té solució en el cos ℝ dels nombres reals.
Cal, doncs, construir un cos que contingui el cos ℝ com a subcòs i alhora un element i que compleixi i 2 + 1 = 0 Per fer-ho és possible procedir de dues formes D’una banda, és possible de considerar el pla complex D’una altra, és possible de considerar l’anell quocient ℂ = ℝ X / x 2 + 1, on ℝ X és l’anell dels polinomis en la variable X amb coeficients reals i X 2 + 1 és l’ideal engendrat pel polinomi, irreductible a ℝ, X 2 + 1 Hom disposa aleshores de l’aplicació canònica π ℝ X → ℂ i la imatge d’ X és anomenada i És a dir, i = π X Aquest cos té una propietat molt important…
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y…
rotació
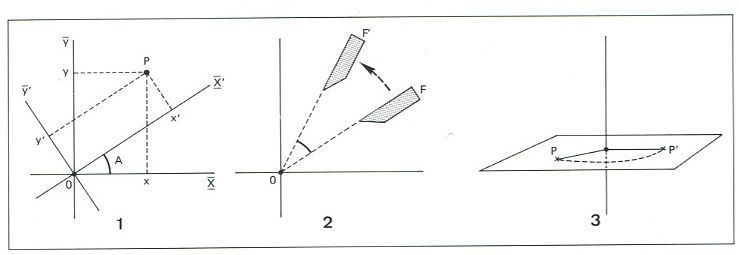
rotació: 1, d'eixos; 2, al voltant d'un punt0; 3, al voltant d'un eix
Matemàtiques
Transformació geomètrica que constitueix un dels moviments rígids del pla o de l’espai i que conserva les distàncies (mides i forma) i l’orientació de les figures sobre les quals és aplicada.
En el pla hom considera la rotació al voltant d’un punt fix que correspon a moviments rígids circulars de centre al punt donat En l’espai hom considera la rotació al voltant d’una línia , en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada eix de rotació, en un pla perpendicular a aquesta i que passa pel punt donat Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser més adequat per a l’estudi d’un problema geomètric concret així,…
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i…
base d’entorns d’un punt
Matemàtiques
Família de conjunts d’un espai topològic, els quals contenen el punt donat, tal que qualsevol conjunt de la topologia que contingui el punt també conté un membre de la família.