Resultats de la cerca
Es mostren 12 resultats
valuació
Matemàtiques
Funció que fa correspondre a cada proposició el seu valor de veritat, si aquest existeix.
En el cas de la lògica binària clàssica els únics valors de veritat que s’admeten són veritat 1 i fals 0, però en les lògiques polivalents hom accepta un tercer valor 1/2 que admet interpretacions diverses per exemple, possible o indeterminat La taula de veritat bivaluada o polivalent de dues proposicions reflecteix totes les possibles valuacions o assignacions de valors de veritat
operació inversa
Matemàtiques
En certes operacions, donat un resultat i un dels factors, aplicació que els fa correspondre l’altre factor.
Per exemple, l’operació inversa de la suma és la resta
singletó
Matemàtiques
Conjunt que conté un únic element.
Anomenat també conjunt unitari , és un concepte bàsic en correspondre a la diferència entre “element” i “subconjunt” així, si a és element d’un conjunt A , aleshores el singletó d' a que hom representa per { a }, és un subconjunt d' A
Jean Robert Argand
Matemàtiques
Matemàtic francès.
Escriví un Essai sur une manière de représenter les quantités imaginaires París, 1806, on establí els diagrames que fan correspondre a cada nombre complex un vector del pla, coneguts per diagrames d’Argand Aplicà aquest mètode a la demostració del teorema fonamental de l’àlgebra
àlef
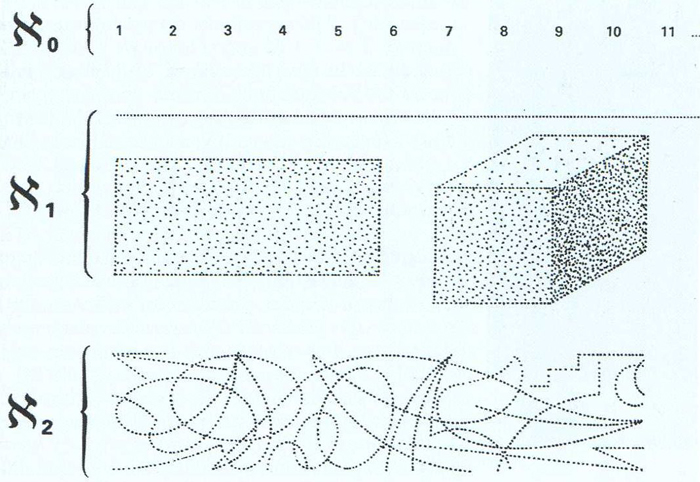
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
diferenciació
Matemàtiques
Aplicació que fa correspondre a cada funció diferenciable en un cert conjunt obert la seva funció diferencial en l’esmentat conjunt.
addició
Matemàtiques
Operació consistent a fer correspondre a cada parell d’elements d’un determinat conjunt un altre element del mateix conjunt, anomenat suma.
La definició específica d’addició varia segons els elements als quals hom la vulgui aplicar Entre nombres naturals, el resultat de l’addició, és a dir, la suma, és el nombre natural que representa el conjunt que és reunió de dos conjunts sense elements comuns que representin els addends Si A té dos elements, A = {a,b}, i B té tres elements, B = {c,d,e}, la reunió A∪B = {a,b,c,d,e} té cinc elements, 2 + 3 = 5 Entre nombres reals, el resultat de l’addició és obtingut sumant o restant els valors absoluts dels addends segons que aquests siguin del mateix signe o de signe contrari El signe de la…
estructura algèbrica
Matemàtiques
Conjunt en què hom ha definit una o unes quantes relacions binàries o lleis de composició.
Una llei de composició interna definida en un conjunt E és una operació que permet de fer correspondre a cadascun dels parells ordenats a, b d’elements, distints o no de E , un element ben determinat del mateix conjunt E Així, doncs, una llei de composició apareix com una aplicació de E × E en E Una estructura és definida, doncs, per mitjà d’un cert nombre d’axiomes que determinen les relacions i les operacions que la componen Les estructures més freqüents en àlgebra són les de grup, anell, cos i espai vectorial
precisió
Física
Matemàtiques
En contraposició amb error, qualitat de fer correspondre amb exactitud el resultat de la mesura experimental d’una magnitud amb el seu valor real.
La precisió no és quantificable quan hom vol conèixer la precisió d’una mesura, en calcula l’error amb què ha estat realitzada
afinitat
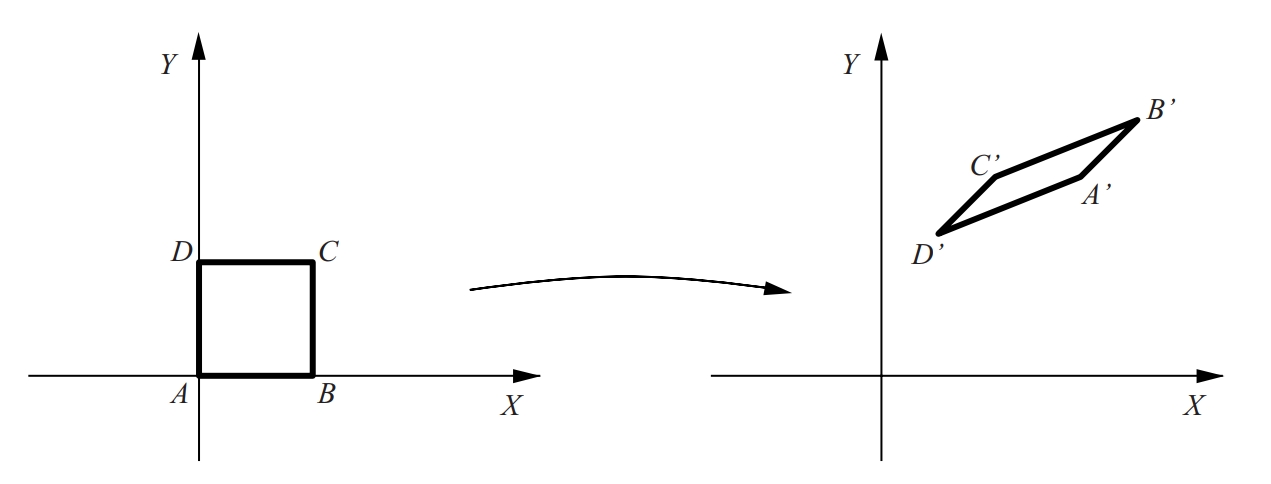
afinitat Transformació afí d’un quadrat
© Fototeca.cat
Matemàtiques
Transformació de l’espai afí en si mateix, que fa correspondre línies paral·leles amb línies paral·leles, punts propis amb punts propis i no canvia el subespai de l’infinit.
Enclou, entre d’altres transformacions, la traslació, la rotació i la simetria Les propietats geomètriques conservades per aquesta transformació són dites afins o lineals llur estudi constitueix la geometria afí