Resultats de la cerca
Es mostren 5 resultats
tríedre de Frenet
Matemàtiques
Tríedre trirectangle constituït pels vectors tangent, normal i binormal a una corba en un punt.
Donada una corba C , parametritzada per l’abscissa curvilínia s s dona la longitud de l’arc des d’un punt de referència de la corba, C s = x s , y s , z s , tríede ortonormal directe definit en cada punt P de C pels vectors tangent t , normal n i binormal b , l’expressió dels quals és t = d C s / ds P , ∥ t ∥=1 n = d t / ds /∥ d t / ds ∥ P , ∥ n ∥=1 b = t ∧ n , ∥ b ∥=1 El pla P , t , n és el pla osculador de la corba C en el punt P , el pla P , n , b és el pla normal de C en P , i el pla P , b , t és el pla rectificador de C en P El radi de…
element de superfície
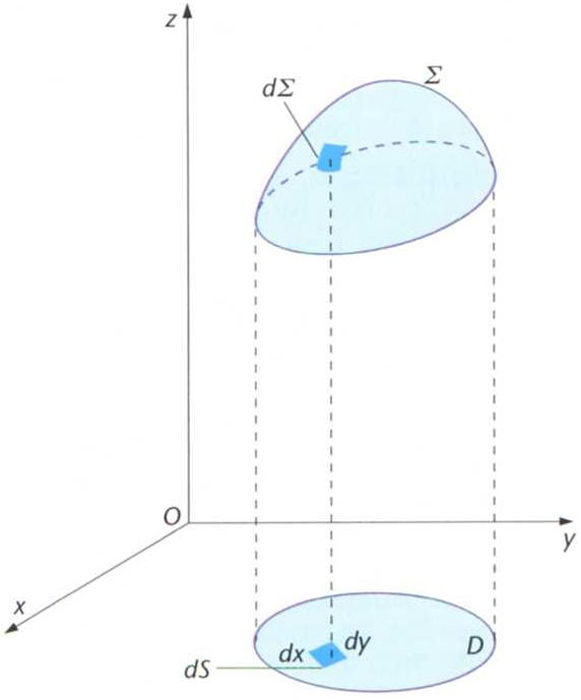
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
torsió d’una corba
Matemàtiques
Valor numèric, definit per a cada punt d’una corba, que val zero en les corbes planes i que expressa quant se separa la corba considerada d’una corba plana en un entorn del punt considerat.
Per a una corba x = x t , y = y t , z = t hom defineix la torsió per la relació τ = | d b / ds|, on ds és la longitud de l’element d’arc ds = { c ' t 2 + y ' t 2 + z ' t 2 } 1 / 2 i b és el vector binormal, és a dir, b = t ∧ n , on t i n són els vectors tangent i normal a la corba, respectivament
flux d’un camp vectorial a través d’una superfície
Matemàtiques
Donat un camp vectorial A i una superfície orientable S, integral de superfície de A sobre S
.
El flux elemental de A a través d’un element de superfície dS és el producte escalar d ϕ= A d S , on d S és el vector normal a dS i de mòdul dS El flux total de A a través de la superfície S és, doncs, Φ=∫∫ s A d S Si S és una superfície tancada que determina un volum V , la fórmula de Gauss o d’Ostrogadskij afirma que Φ = ∫∫ s A d S = ∫∫∫∂ x A x + ∂ y A y + ∂ z A z dV , on A x , A y i A z són les components del camp A
arc
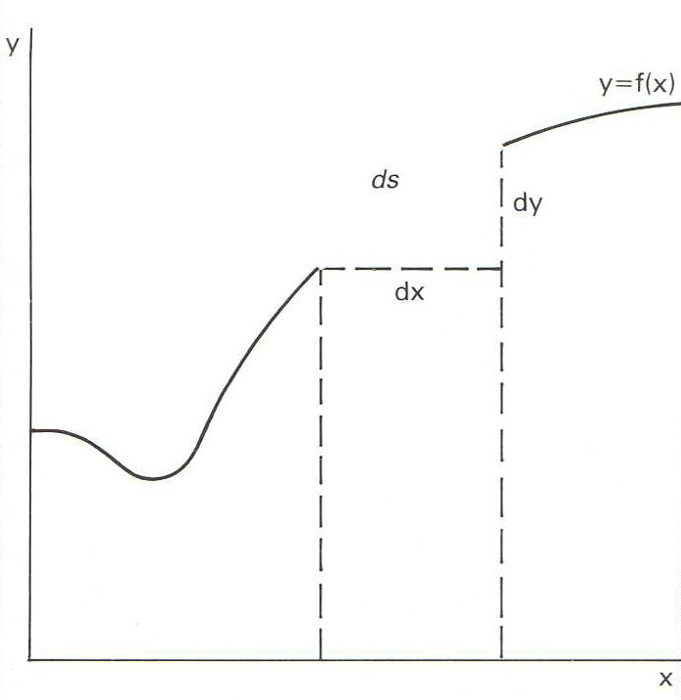
Matemàtiques
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es planteja a propòsit d’un…