Resultats de la cerca
Es mostren 242 resultats
Elements
Matemàtiques
Tractat de matemàtiques atribuït a Euclides i que ha estat, fins a mitjan segle XIX, l’autoritat màxima dins el camp de les matemàtiques generals.
Sintetitzà perfectament el treball dels antics matemàtics grecs i li donà una major coherència lògica amb les noves definicions de línia i de pla i, sobretot, amb la introducció del cinquè postulat millorà també l’ordenació i les demostracions de les proposicions Malgrat ésser un text de compilació, hom no pot posar en dubte que la planificació global de l’obra i el mètode expositiu, com també un bon nombre dels seus teoremes, són obra del mateix Euclides
mètode dels elements finits
Matemàtiques
Mètode numèric per a resoldre problemes d’equacions diferencials en derivades parcials.
Matemàticament és una extensió de la tècnica de Rayleigh-Ritz-Galerkin el problema es planteja en forma variacional i hom aproxima la solució mitjançant una combinació lineal de funcions senzilles, en aquest cas funcions polinòmiques a trossos, nulles excepte en un petit domini dintre del qual són polinomis de grau baix El mètode aparegué els anys seixanta entorn de l’aplicació dels ordinadors als càlculs elàstics d’estructures, superà molt de pressa els mètodes de diferències finites i amplià ràpidament el seu camp d’aplicacions i es mostrà molt potent especialment quan la geometria del…
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…
conjunt finit
Matemàtiques
Conjunt amb un nombre finit d’elements.
Formalment, és un conjunt equipotent a un nombre natural necessàriament únic que compta els elements del conjunt Equivalentment, un conjunt és finit quan el seu cardinal és un nombre natural
descomposició en factors irreductibles
Matemàtiques
Descomposició característica dels elements d’un tipus d’anell, anomenat anell factorial
.
Un anell factorial A és un anell commutatiu unitari i íntegre el producte de dos elements no nuls no és nul en què tot element x no nul i no invertible pot ésser expressat d’una manera única en la forma x = up 1 p n , on u és un element invertible de A i els p i i = 1,, n són elements irreductibles de A elements p no invertibles de A tal que si p = ab aleshores almenys un dels factors, a o b , és invertible
matriu
Matemàtiques
Disposició dels elements d’un cos K
de la manera següent
.
Segons que el cos K sigui el dels nombres reals o el dels nombres complexos, hom parla de matriu real o de matriu complexa , respectivament Cadascuna de les línies horitzontals de nombres és una fila de la matriu, i cada línia vertical de nombres n'és una columna En l’exemple donat, la matriu A té files i columnes hom diu que A és una matriu m × n El conjunt de les matrius m ×és notat per M m X n K Una matriu pot ésser expressada també mitjançant el seu element genèric a i j , en la forma A = a i j Aquí, és l' índex de fila i j és l' índex de columna La fila formada pels elements…
permutació
Matemàtiques
Aplicació d’un conjunt de n elements a n llocs diferents, és a dir, cadascun dels diferents arranjaments lineals que es poden fer amb diferents elements, entrant tots ells en cadascun dels arranjaments.
El nombre de permutacions diferents que hom pot fer amb un conjunt de n elements és n n factorial i és donat per la fórmula n = n n- 1 n -2 2 × 1 Si hom identifica alguns dels elements del conjunt, obté les permutacions amb repetició Si el conjunt és identificat en classes de n 1 , n 2 n r elements, el nombre de permutacions amb repetició és n / n 1 n 2 n r Si hom suposa que els llocs són disposats en un cercle i que no es distingeix entre dues permutacions si només difereixen en una rotació, hom obté les permutacions circulars , tant amb…
perspectiva axonomètrica
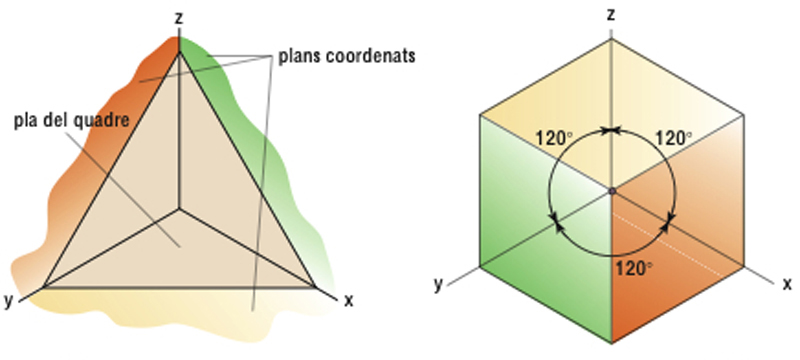
Elements de la perspectiva axonomètrica (isomètrica) i representació d’un cub
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Sistema de representació que consisteix a referir els objectes que han d’ésser representats —mitjançant projeccions ortogonals— als plans d’un tríedre trirectangle ( plans coordenats
) i projectar-los, després, sobre un quart pla ( pla del quadre
) oblic als anteriors ( axonometria
).
El seu traçat es redueix a dibuixar les direccions dels cossos parallelament a la projecció dels eixos coordenats, relacionant amb ells les mesures d’alçada, amplada i profunditat Definit el pla del quadre, les projeccions de les arestes del tríedre sobre el pla no són donades en llurs veritables magnituds, sinó que tindran una magnitud menor Això equival a dir que totes les línies de l’espai paralleles a un pla del tríedre es veuran reduïdes en la mateixa proporció La relació entre la magnitud sobre el pla del quadre d’una de les arestes i la seva veritable magnitud és denominada coeficient…
relació d’ordre
Matemàtiques
Relació binària R entre els elements d’un conjunt C que és reflexiva, antisimètrica i transitiva.
La parella C, R constitueix un conjunt ordenat És usual la notació ≤per a designar la relació d’ordre desigualtat 5, i a ≤ b és llegit '' a menor o igual a b' , o bé '' a inferior a b' aquesta notació generalitza la coneguda i usual relació “ésser menor que o igual a” que ordena els nombres Unes altres relacions d’ordre importants són la relació d’igualtat, la relació d’inclusió entre conjunts, la relació “ésser divisor de” en els nombres naturals, etc En un conjunt ordenat, són elements notables el màxim , el mínim , el maximal , el minimal , el majorant i el minorant Dos…
grup simètric d’un conjunt
Matemàtiques
Donat un conjunt C, grup S(C) els elements del qual són les permutacions dels elements de C i l’operació interna del qual és la composició d’aplicacions.
Si C = {1,, n }, el corresponent grup simètric és l’anomenat grup simètric de n elements, i és notat per S n
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina