Resultats de la cerca
Es mostren 141 resultats
sistema d’equacions
Matemàtiques
Conjunt d’equacions que han d’ésser satisfetes per un mateix conjunt de valors de les variables.
Si les equacions del sistema són totes de primer grau sistemes lineals la discussió i la resolució són obtingudes pel teorema de Rouché-Frobenius i la regla de Cramer
sistema d’equacions lineals
Matemàtiques
Conjunt d’equacions lineals de les quals interessen les solucions comunes.
Un sistema d’aquest tipus és anomenat compatible si admet solució, i incompatible en el cas contrari Un sistema compatible és determinat si la solució és única, i indeterminat si, per contra, hi ha infinites solucions Els sistemes d’equacions lineals són anomenats no homogenis si els termes independents b 1 , b m no són tots nuls, i homogenis en el cas contrari La regla de Cramer permet, mitjançant l’ús dels determinants, de resoldre els sistemes de 3 equacions amb 3 incògnites té solució on és el determinant del sistema, que ha d’ésser no nul
equacions d’Einstein-Lorentz
Matemàtiques
Si hom considera dos observadors que es mouen amb velocitat relativa v en la direcció d’un eix comú que hom pren com a eix de les ics, la posició i el temps en què s’esdevé un succés P seran amidats per un observador en funció de les coordenades x, y, z i del temps t i, per l’altre, en funció d'x', y', z' i t', dependents del seu sistema referencial.
Les equacions d’Einstein-Lorentz estableixen el lligam que hi ha entre aquestes dues quaternes de nombres i són que admeten la transformació inversa que hom obté canviant x , y , z , t per x ', y' , z' , t' i canviant el signe de v És d’interès observar que 1/ c = 0 proporciona la transformació clàssica o galileana Dit altrament, si v és força negligible davant de la velocitat c de la llum, aleshores la transformació d’Einstein-Lorentz esdevé la transformació de la mecànica clàssica Cal remarcar, finalment, que les transformacions d’Einstein-Lorentz conserven la forma de l’…
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta d’un sistema compatible indeterminat…
teoria
Matemàtiques
Conjunt de principis referents a un determinat concepte (o conceptes) que inclou tant els axiomes postulats sobre aquest com les conseqüències (teoremes) que d’aquests axiomes han estat deduïdes lògicament.
Així, la teoria de funcions estudia les funcions reals o les complexes funció la teoria d’equacions estudia els mètodes de resoldre equacions, les relacions entre les solucions i les que hi ha entre aquestes i els coeficients de les equacions equació Cal esmentar també altres teories d’una gran importància, com la teoria de grups grup, la de conjunts conjunt, la de nombres nombre, la dels jocs , la de probabilitats probabilitat, la de catàstrofes catàstrofe, la de sistemes sistema, etc
equació diferencial
Matemàtiques
Equació funcional (en el sentit que les incògnites són funcions) on apareixen les derivades de la funció incògnita.
Si la funció és d’una sola variable, l’equació és una equació diferencial ordinària Per tal que aquesta definició, molt general, no inclogui certes classes d’equacions especials com és ara les equacions diferencials en diferències f ´ x = f x + h , hom precisa que la funció incògnita i les seves derivades tan sols poden ésser sotmeses a operacions algèbriques El tipus general d’equació diferencial és escrit F t,x,x´,,x n = 0 Hom defineix l' ordre d’una equació diferencial com el de la màxima derivada que apareix en l’equació Si F té forma polinòmica, hom parla…
corba
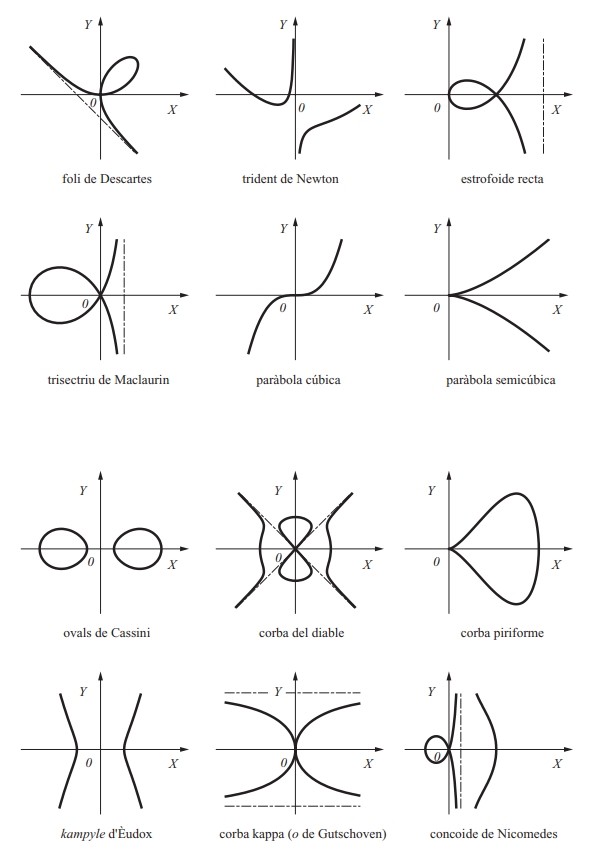
Corbes cúbiques i quàrtiques
Matemàtiques
Lloc geomètric que és la trajectòria d’un punt que es mou amb un sol grau de llibertat.
Una corba sempre pot ser considerada com una infinitat simple de punts, i aquest és el plantejament adoptat pels matemàtics en l’estudi de les corbes contínues topologia En aquest sentit, una corba és el conjunt de punts de ℝ n que és homeomorf amb un interval a , b ⊂ ℝ Seguint Menger hom podria considerar les corbes al pla espai com a objectes de dimensió topològica 1 ja que tota circumferència superfície esfèrica de centre un punt de la corba la talla en un conjunt de punts de dimensió zero punts que són centres de circumferències superfícies esfèriques que no contenen altres punts del…
Erik Ivar Fredholm
Matemàtiques
Matemàtic suec.
Fou professor de física matemàtica a la Universitat d’Estocolm Féu nombroses investigacions sobre equacions funcionals i equacions integrals i mecànica i física matemàtica
Issai Schur
Matemàtiques
Matemàtic alemany d’origen rus.
Estudià i treballà a la Universitat de Berlín fins que, el 1935, hagué d’abandonar-la pressionat pels nazis Féu contribucions en teoria de grups, de matrius, equacions algèbriques, equacions integrals, etc
transformada de Laplace
Física
Matemàtiques
Donada una funció real f tal que f(t) = 0 per a t<0, funció F(s) definida per l’expressió F(s) = ∫∞0f(t) e-st dt, essent s un nombre complex.
Hom la designa sovint per ℒ f , o bé per ℒ f , i permet de transformar equacions diferencials de difícil resolució en equacions algèbriques És emprada especialment per a l’anàlisi de circuits elèctrics i de servosistemes
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina