Resultats de la cerca
Es mostren 10 resultats
punt de retrocés
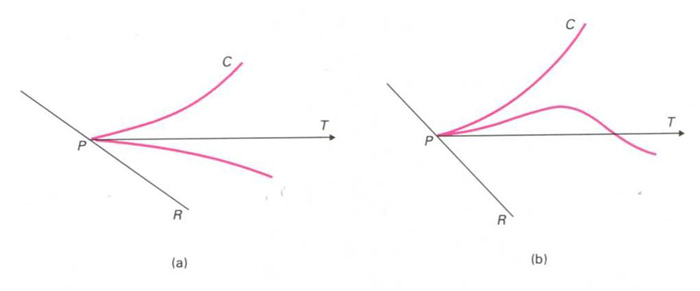
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
discontinuïtat
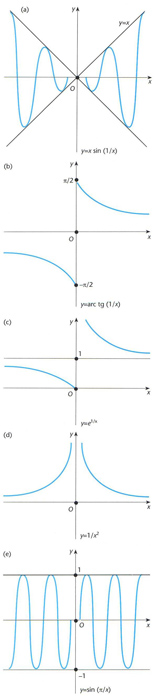
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…
mesura
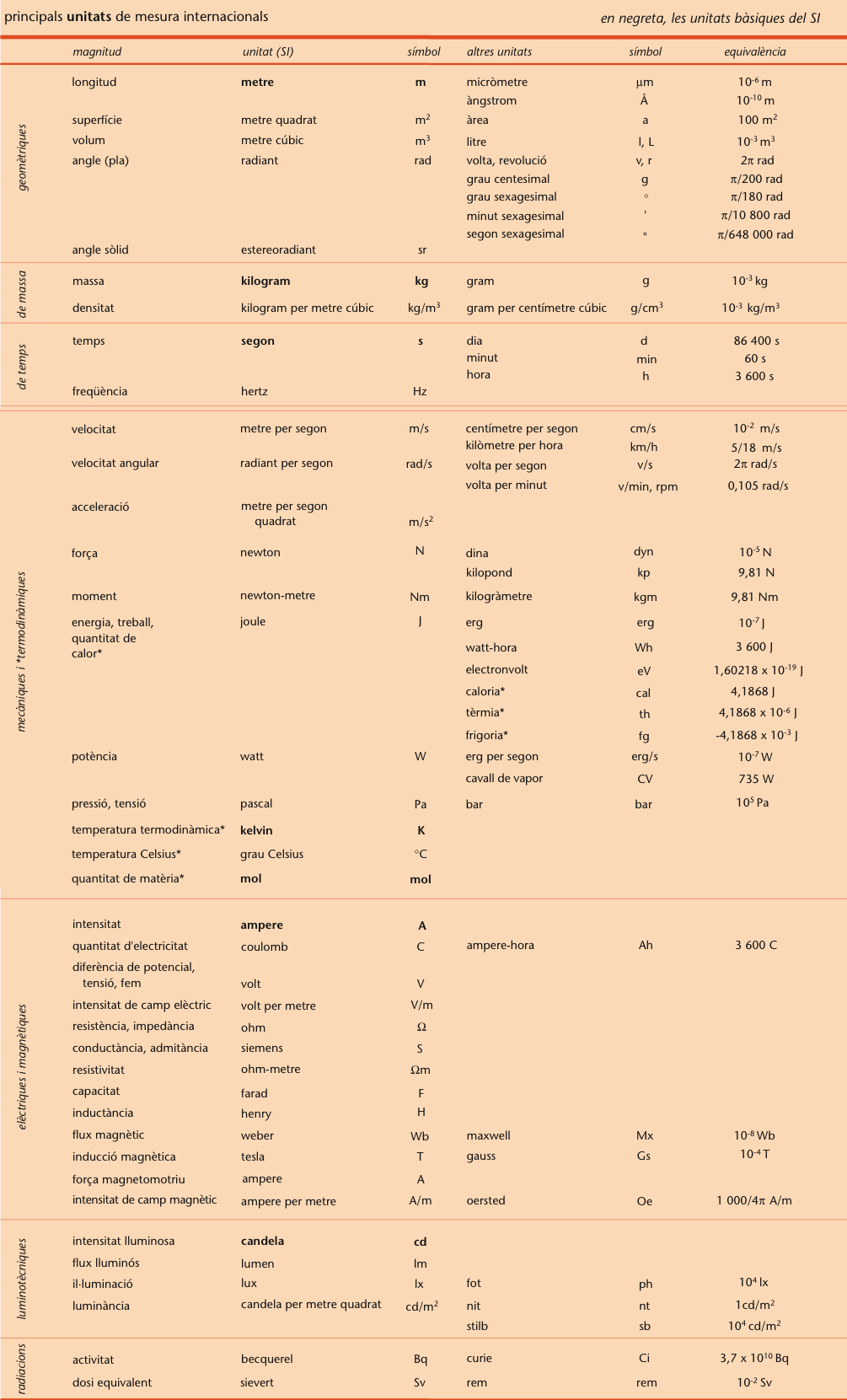
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són…
contrast d’hipòtesi
Matemàtiques
Prova que consisteix en la realització d’experiències que permetin de determinar el valor d’una variable aleatòria definida en funció de la hipòtesi formulada en termes estadístics.
Prèviament hom ha d’estudiar la llei de probabilitat d’aquesta variable aleatòria per tal de fixar uns límits més enllà dels quals la probabilitat sigui negligible si el resultat de les experiències dóna per a la variable un valor comprès dins aquests límits, hom considera acceptable la hipòtesi H 0 , anomenada hipòtesi nulla , sense que això vulgui dir que és certa, sinó només que res no s’oposa a tenir-la per certa d’acord amb la informació obtinguda Altrament hom preferirà l’anomenada hipòtesi alternativa H 1 , única o diversa, diferent de la primera Cadascuna de les dues decisions…
funció esglaonada
Matemàtiques
Funció f: [a, b] ⊂ℝ → Osb; tal que existeix una subdivisió del seu interval de definició, a=a0 < a1 < ... < an = b, tal que les restriccions de f a cada interval obert (ai - 1, ai) és una funció constant.
Els punts a i són discontinuïtats de primera espècie
funció contínua a trossos
Matemàtiques
Funció f:[a,b]⊂ℝ→ℝtal que existeix una subdivisió del seu interval de definició, a=a0 <a1 <...<an =b, tal que, per a tot i=1,...
, n , existeix una funció f i contínua en l’interval tancat a i - 1 , a i i igual a f en l’interval obert a i - 1 ,a i Les discontinuïtats de són discontinuïtats de primera espècie discontinuïtat
factor
Matemàtiques
Nombre que expressa el quocient de dues magnituds de la mateixa espècie, per la qual cosa és adimensional.
Aquesta definició estricta no ha estat sempre aplicada, i hom confon sovint els factors amb els coeficients
test d’hipòtesis estadístiques
Matemàtiques
Donada una mostra de grandària n, ( x1,...,xn ), formada per n realitzacions o observacions independents d’un cert fenomen o experiment.
Aquest mètode permet de decidir, a partir de les dades observades, si una hipòtesi estadística que hom ha fet sobre el model probabilístic del fenomen és correcta o no ho és Aquesta decisió hauria d’ésser presa sempre amb un cert grau d’incertesa Els problemes que tracta de resoldre aquesta teoria poden ésser, per exemple, decidir quin dels dos mètodes diferents de fabricació de bombetes elèctriques dona una mida mitjana més gran, o bé saber, a partir d’una sèrie d’anàlisis, si un malalt té una certa malaltia Sovint el model probabilístic consisteix en una llei de probabilitat teòrica donada…
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…