Resultats de la cerca
Es mostren 15 resultats
funció estrictament monòtona
Matemàtiques
Funció estrictament creixent o estrictament decreixent (creixent, decreixent).
funció decreixent
Matemàtiques
Funció f(x) tal que x≤y⇒f(x)≥f(y).
És estrictament decreixent si x < y ⇒ f x > f y
funció creixent
Matemàtiques
Funció f(x) tal que x≤y⇒f(x≤f(y).
És estrictament creixent si x < y ⇒ f x < f y
àlef
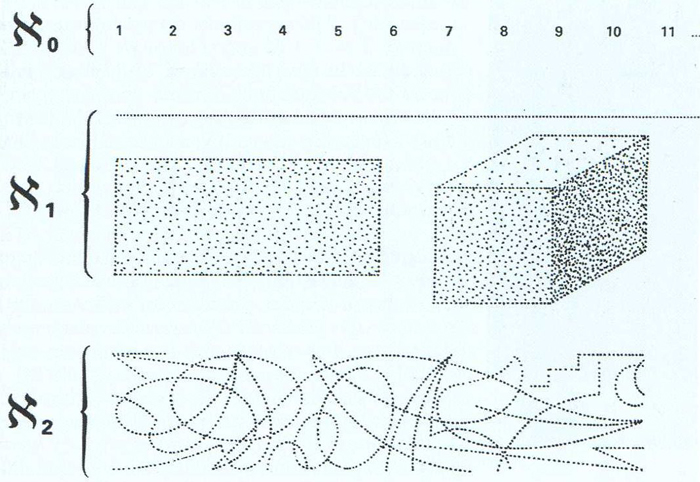
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
inclusió estricta
Matemàtiques
Relació d’ordre estricte entre conjunts.
Es nota mitjançant el símbol ℮ o mitjançant ⊂ si hom empra el símbol ⊆ per a la inclusió no estricta, definida per la condició A ℮ B o, respectivament A ⊂ B si i només si tots els elements de A pertanyen a B però A no és igual a B és a dir B té elements altres que els de A En aquest cas, hom diu que el conjunt A és inclòs estrictament en el conjunt B o que A és un subconjunt estricte de B
símplex
Matemàtiques
Conjunt format per n + 1 punts p 0, p 1, ..., Pn linealment independents d’un espai euclidià de dimensió major que n i tots els punts de la forma x =λopo + λ 1p1 + ...
+ λ npn , on λ 0 + λ 1 + + λ n = 1 i 0 ≤λ i , per a cada i Els coeficients λ 0 , λ 1 , , λ n són anomenats coordenades baricèntriques del punt x , el qual pot ésser interpretat com el centre de masses de la distribució determinada en posar pesos λ 0 , λ 1 , , λ n en els punts p 0 , p 1 , , pi Aquest símplex és dit també n-símplex tancat , a fi de distingir-lo del n-símplex obert , en el qual totes les coordenades baricèntriques són estrictament positives Un símplex és degenerat si els punts determinants no són independents Els punts pi són dits vèrtexs i cada collecció de r +…
descomposició d’un polinomi
Matemàtiques
Expressió d’un polinomi com a producte de polinomis de grau menor.
Si K és un cos i K x és l’anell de polinomis sobre K , hom diu que un polinomi p x és reductible sobre K si admet una descomposició en la forma p x = f x g x on grau f x < grau p x en cas contrari hom diu que p x és irreductible o primer sobre K La reductibilitat d’un polinomi depèn del cos a què pertanyen els coeficients així, el polinomi x 2 +1 és reductible sobre ℂ, ja que x 2 +1= x + i x - i , però és irreductible sobre ℝ, perquè no hi admet cap descomposició en factors de grau menor Tot polinomi de l’anell K x pot descompondre’s unívocament en un producte de…
hipòtesi del continu
Matemàtiques
Nom donat a la proposició que afirma que no hi ha cap conjunt el cardinal del qual estigui comprès estrictament entre card (ℕ) i card (ℝ).
És considerada una proposició indecidible
distància
Matemàtiques
Donat un conjunt E
, aplicació d
: Ex
E →ℝ +
que satisfà els següents axiomes:
o sia, la distància és estrictament positiva, simètrica i compleix la desigualtat triangular.
Tot conjunt E en el qual hi ha definida una distància d és un espai mètric , i d és la mètrica de l’espai Per exemple, en el conjunt dels números reals ℝhom pot considerar d x,y = | x — y |, valor absolut de la diferència x — y , on x,y ∈ℝ
derivada a l’esquerra d’una funció en un punt
Matemàtiques
Donada una funció f:D ⊂ℝ→ℝi un punt a∈D, límit, si existeix, del quocient [f(a+h) - f(a)]/h, quan h tendeix a zero mantenint-se estrictament negatiu, h < 0.
Hom empra aleshores la notació f´ e a