Resultats de la cerca
Es mostren 19 resultats
foli de Descartes
Foli de Descartes
© fototeca.cat
Matemàtiques
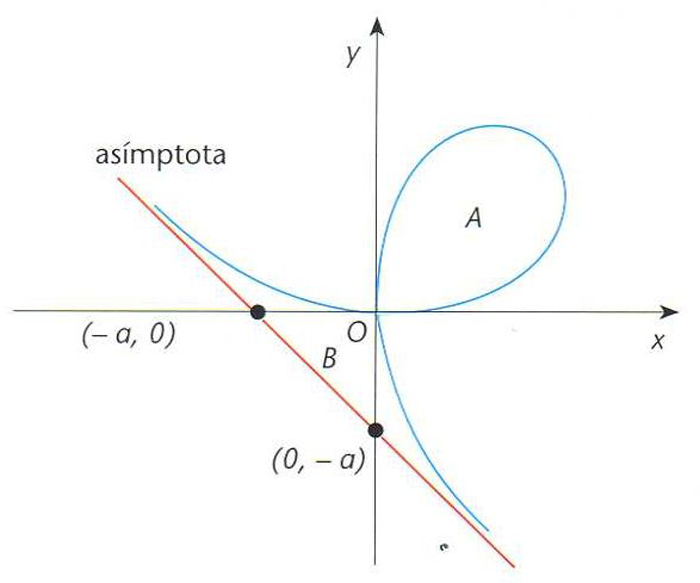
Cúbica expressada implícitament per l’equació cartesiana x3+y3=3axy, on a és una constant.
En forma paramètrica és expressada per x=3at|1+t 3 i y=3at 2 |1+t 3 La recta traçada pels punts de coordenades - a , 0 i 0, -a és una asímptota de la corba L’àrea A limitada pel llaç és igual a l’àrea B compresa entre les dues branques infinites i la asímptota esmentada
lemniscata
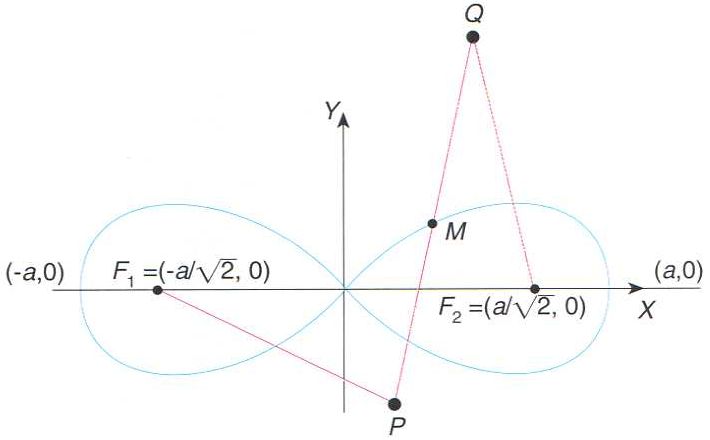
Contrucció geomètrica de lemniscata: ès el lloc geomètric dels punts M situats al mig d’un segment de longuitud constant, que uneixen dos punts, P i Q, que descriuen circumferències de radis a i de centres en el focus F1 i F2
© Fototeca.cat
Matemàtiques
Corba algèbrica de quart grau que té una forma semblant a la d’un vuit.
És coneguda també com a lemniscata de Bernoulli , i pot ésser expressada per l’equació x 2 + y 2 2 = a 2 x 2 - y 2
funció racional
Matemàtiques
Funció expressada pel quocient de dues funcions polinòmiques.
element de superfície
Element de superfície
© fototeca.cat
Matemàtiques
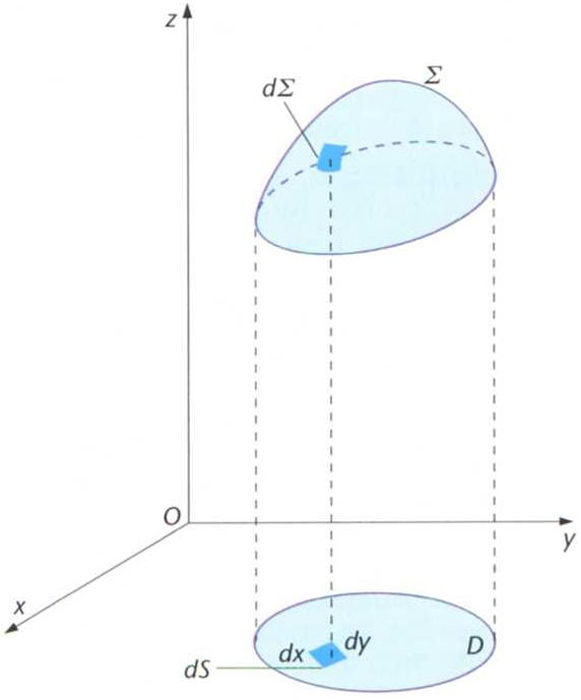
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
derivació sota el signe integral
Matemàtiques
Derivació d’una funció expressada mitjançant una expressió integral.
Així, si fx = ∫ b a F x,y dy, aleshores la seva derivada és donada per l’expressió integral f'x = ∫ b a ∂F x,y /∂ x dy Aquesta forma d’obtenir la derivada és anomenada regla de Leibniz
norma
Matemàtiques
En els espais vectorials de dimensió 1, 2 o 3 (recta, pla, espai ordinari), longitud d’un vector.
Si el vector és determinat per les seves components en un sistema de coordenades ortonormals eixos perpendiculars i unitats iguals sobre cada eix, la norma del vector v = x 1 , x 2 , x 3 és expressada així Per mitjà del producte escalar, és D’aquesta manera la noció de norma s’estén a espais vectorials de dimensió qualsevol, finita o infinita La norma té en tot cas les propietats de la distància, és a dir, és positiva o nulla, només el vector zero té norma nulla, i satisfà la desigualtat triangular,
equació irreductible
Matemàtiques
Equació expressada per un polinomi irreductible descomposició d'un polinomi.
teorema de Pitàgores
Matemàtiques
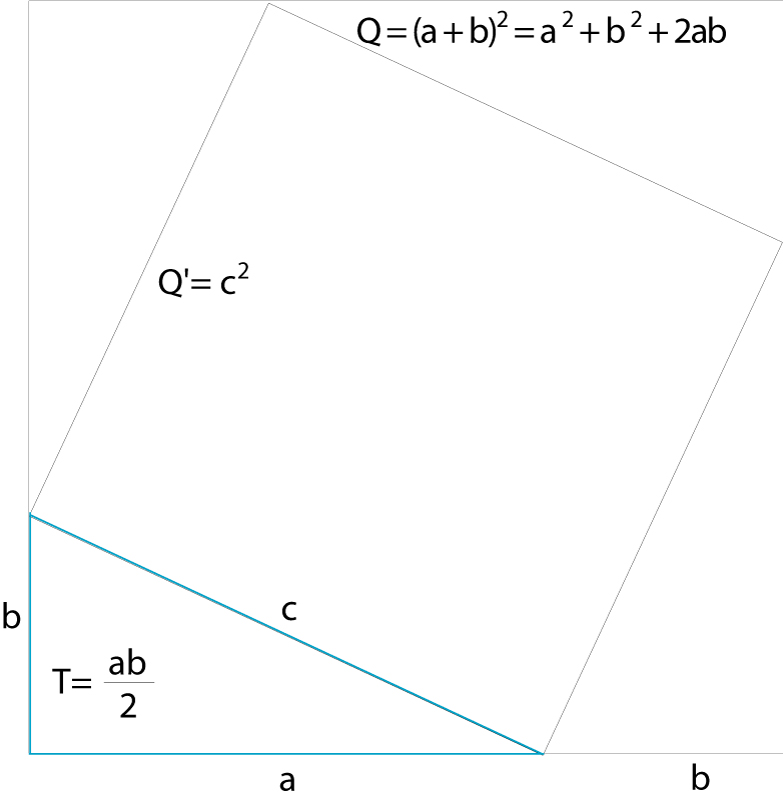
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris per a mesurar…
equació de Laplace
Física
Matemàtiques
Equació diferencial en derivades parcials expressada per la fórmula Δf = 0, Δ essent el laplacià.
Les funcions que són solució de l’equació de Laplace són anomenades funcions harmòniques , i tenen una especial aplicació en la teoria del potencial En el cas que f sigui una funció de la variable complexa z = x + iy , l’equació de Laplace, que en aquest cas pren la forma ∂ 2 f /∂ x 2 + ∂ 2 f /∂ y 2 = 0, expressa la condició necessària i suficient perquè f sigui derivable
rotació
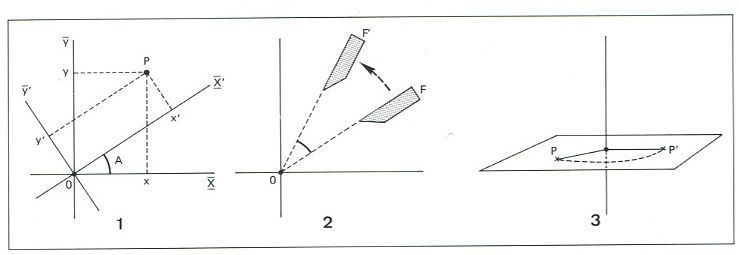
rotació: 1, d'eixos; 2, al voltant d'un punt0; 3, al voltant d'un eix
Matemàtiques
Transformació geomètrica que constitueix un dels moviments rígids del pla o de l’espai i que conserva les distàncies (mides i forma) i l’orientació de les figures sobre les quals és aplicada.
En el pla hom considera la rotació al voltant d’un punt fix que correspon a moviments rígids circulars de centre al punt donat En l’espai hom considera la rotació al voltant d’una línia , en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada eix de rotació, en un pla perpendicular a aquesta i que passa pel punt donat Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser més adequat per a l’estudi d’un problema geomètric concret així,…