Resultats de la cerca
Es mostren 11 resultats
freqüència
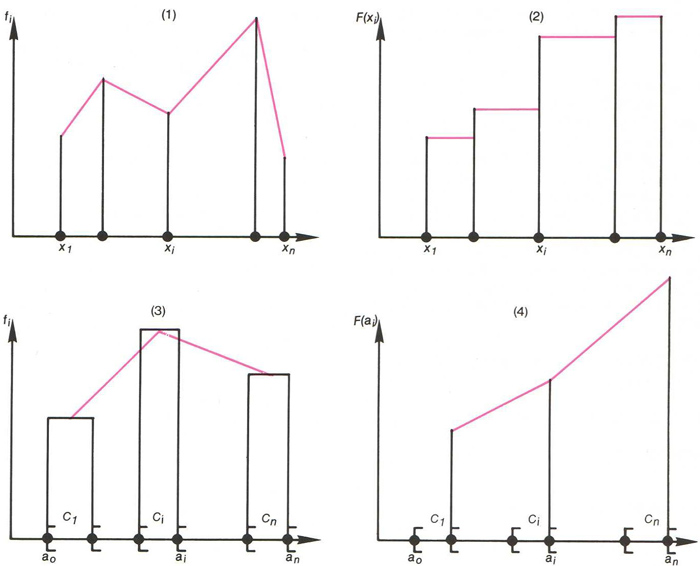
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1…
freqüència
Matemàtiques
En una sèrie de N repeticions d’una experiència en què hom estudia la realització o no realització d’un esdeveniment A, quocient entre el nombre d’esdeveniments en què A es realitza i el nombre total d’esdeveniments, N: f=n/N
.
El nombre f és la freqüència o freqüència relativa de l’esdeveniment A
freqüència cumulativa
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, suma de les freqüències dels valors del caràcter, o de les classes de valors del caràcter, anteriors al valor que caracteritza la freqüència cumulativa en qüestió.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,, x n , la freqüència cumulativa del valor x i és el nombre on f j és la freqüència del valor x j La representació gràfica de la funció x i → F x i és una corba esglaonada anomenada corba cumulativa o corba de freqüències cumulatives Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de valors del caràcter, la freqüència cumulativa del valor a i o de la classe C i és el nombre on f j és la freqüència de la classe C j La…
teorema de Bernoulli
Matemàtiques
Donat un nombre ε arbitràriament petit, la probabilitat que la diferència entre la freqüència relaiva f de l’esdeveniment favorable en una sèrie de proves i la probabilitat p d’aquest esdeveniment sigui, en valor absolut, superior a ε tendeix a zero en augmentar indefinidament el nombre de proves.
O sigui Aquest teorema fa aparèixer el lligam que hi ha entre freqüència relativa i probabilitat, la qual és el valor mitjà de la freqüència per a un nombre molt gran de proves Com que hi intervé un nombre de proves tant gros, aquest teorema és conegut també amb el nom de llei dels grans nombres
histograma
Matemàtiques
Representació gràfica, formada per rectangles, de les freqüències d’una variable.
Quan la variable pren valors discrets, tots els rectangles tenen la mateixa amplada i llur altura és proporcional a la freqüència corresponent al punt on el rectangle és situat Quan la variable és contínua, els rectangles són contigus i l’àrea de cadascun d’ells, que té per base un cert interval de la variable, és proporcional al valor global de la freqüència corresponent a l’interval
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que…
harmònic
Física
Matemàtiques
Cadascun dels termes de la sèrie de Fourier d’una funció periòdica (anàlisi de Fourier).
El terme de la sèrie de freqüència més baixa és anomenat harmònic fonamental o primer harmònic , i els altres termes són anomenats harmònics del fonamental
agrupament de classes
Matemàtiques
Divisió de l’interval que comprèn totes les observacions d’una sèrie estadística en petits intervals iguals.
Cada un d’aquests intervals constitueix una classe, i hom atribueix el valor mitjà de l’interval a totes les observacions que conté El nombre d’observacions dins un interval és anomenat freqüència d’aquest interval
Andrej Andrejevič Markov
Matemàtiques
Matemàtic rus, deixeble de P.L. Čebyšev.
Fou un dels membres més destacats de l’escola de matemàtics russos dedicats a l’estudi de la teoria de probabilitats Treballà especialment en la llei dels grans nombres, i analitzà els processos estocàstics, els quals considerà com una cadena de proves, que ha estat anomenada cadena de Markov Aplicà els seus coneixements matemàtics a la lingüística anàlisi de Markov per a estudiar la freqüència dels mots i de llurs encadenaments
llei dels grans nombres
Matemàtiques
Teorema intuït per Jakob Bernoulli i P.S.Laplace i batejat així per S.D.Poisson, la demostració del qual, progressivament més i més rigorosa, començà amb P.L.Čebyšev i ha acabat amb E.F.E.Borel, Khinčin, A.N.Kolmogorov, Glivenko i Cantelli.
Una primera formulació de la llei dels grans nombres és la llei feble dels grans nombres , anomenada també teorema de Bernoulli, que estableix que la freqüència relativa d’un esdeveniment al llarg de n temptatives elementals independents convergeix en probabilitat vers la probabilitat de l’esdeveniment Hom diu que una variable aleatòria X n convergeix en probabilitat vers una variable certa A quan la diferència | X n —A | tendeix a 0 en augmentar n , és a dir, quan ε essent tan petit com hom vulgui Una altra formulació de la llei dels grans nombres és l’anomenada llei forta dels…