Resultats de la cerca
Es mostren 50 resultats
grup cíclic
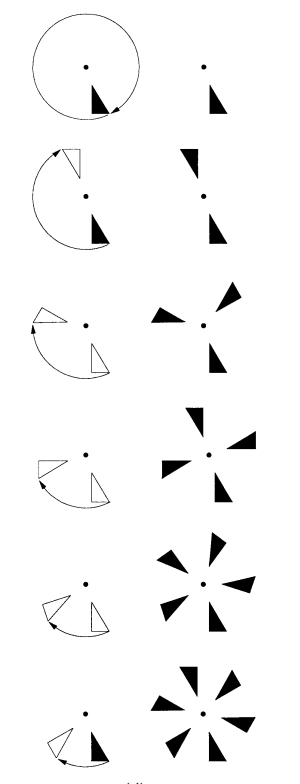
grups cíclics
© Fototeca.cat
Matemàtiques
Grup abelià G format per totes les potències enteres d’un element g, anomenat generador de G. Per exemple, el grup dels enters (ℤ, +) és un grup cíclic de generador el número 1.
grup dièdric
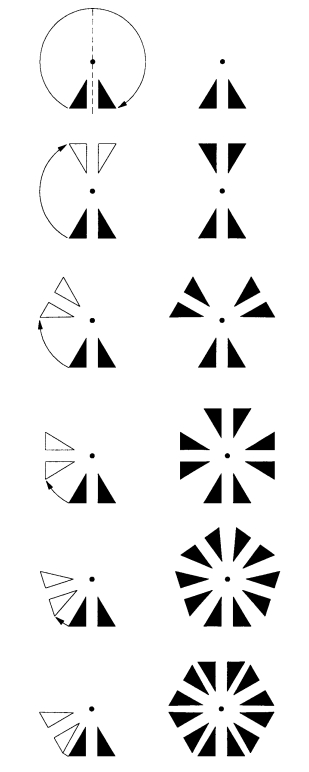
grups dièdrics
© Fototeca.cat
Matemàtiques
Grup de transformacions format pels girs i simetries que deixen invariant un polígon regular.
grup de simetria

Els disset grups de simetria del pla
© Fototeca.cat
Matemàtiques
Grup format per totes les isometries que deixen invariant una certa figura.
aleatorització
Matemàtiques
Procediment que consisteix a assignar a l’atzar els participants d’un estudi en diferents grups.
L’aleatorització assegura la teòrica impredictibilitat de l’assignació dels participants als diferents grups d’intervenció de l’estudi que tots els participants tinguin la mateixa probabilitat de ser assignats i, finalment, contribueix a fer que els possibles factors de variabilitat entre els participants es distribueixin de manera aleatòria entre els diferents grups d’estudi Aquest procediment s’efectua mitjançant l’assignació dels individus segons una taula de nombres aleatoris
àlgebra de Lie
Matemàtiques
Estructura algebraica l’ús principal de la qual resideix en l’estudi d’objectes geomètrics com ara grups de Lie i varietats diferenciables.
Àlgebra E tal que la seva llei de composició x , y compleix les dues propietats següents per a tot x ∈ E , x , x = 0 i, per a cada terna x , y , z ∈ E , x , y , z + y , z , x + z , x , y = 0 Un exemple d’àlgebra de Lie el constitueix l’espai ℝ 3 dotat del producte vectorial L’estudi d’aquestes àlgebres és important per a l’estudi dels grups de Lie, ja que, a cada grup de Lie, se li pot associar una àlgebra de Lie
conjectures de Burnside
Matemàtiques
Conjunt de problemes algèbrics relatius als grups, plantejats per W.S.Burnside.
D’una banda, es preguntà si tot grup engendrat per un nombre finit d’elements i en el qual tot element és d’ordre finit és necessàriament finit aquesta conjectura fou resposta negativament per Novikov el 1959 D’altra banda, demostrà que si p i q són enters primers diferents, aleshores tot grup d’ordre p 2 q és grup resoluble
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats…
simetria
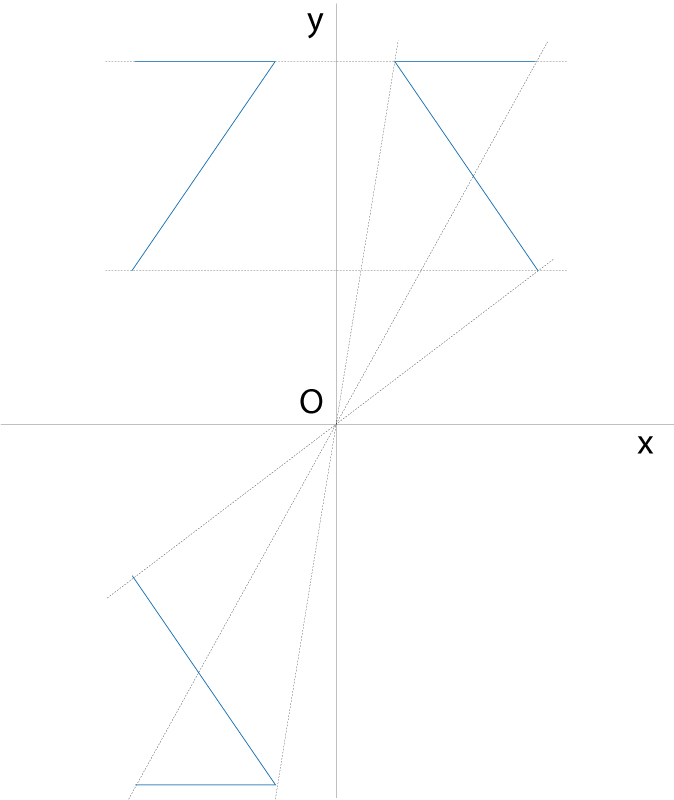
Dues figures obtingudes per simetria axial i central
© Fototeca.cat
Matemàtiques
Configuració d’un objecte que és invariant per a determinats moviments geomètrics.
Dins el concepte de simetria hom estudia modernament tots el moviments geomètrics del pla i de l’espai Una simetria axial és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a una recta donada dita eix de simetria i les distàncies de P a l’eix i de P' a l’eix són iguals Una simetria especular és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a un pla donat dit pla de simetria i les distàncies de P al pla i de P' al pla són iguals Una simetria central és una rotació de 180°…
William Snow Burnside
Matemàtiques
Matemàtic anglès.
Enuncià un gran nombre de problemes de la teoria de grups Desenvolupà, juntament amb Frobenius i Schur, la teoria de les representacions lineals dels grups
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per exemple, la categoria dels grups…