Resultats de la cerca
Es mostren 43 resultats
imatge recíproca d’un element respecte a una aplicació
Matemàtiques
Donat un element y de la imatge d’una aplicació f, conjunt format pels elements x del recorregut de f tals que f(x) = y
.
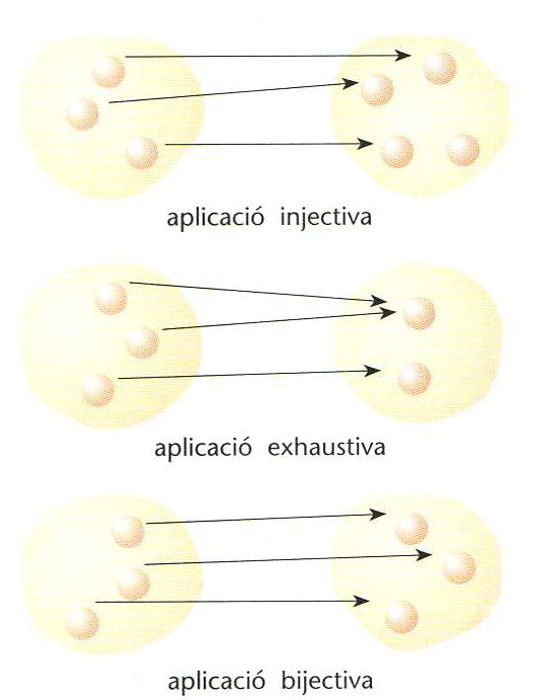
aplicació
fototeca.cat
©
Matemàtiques
correspondència
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta…
fractal
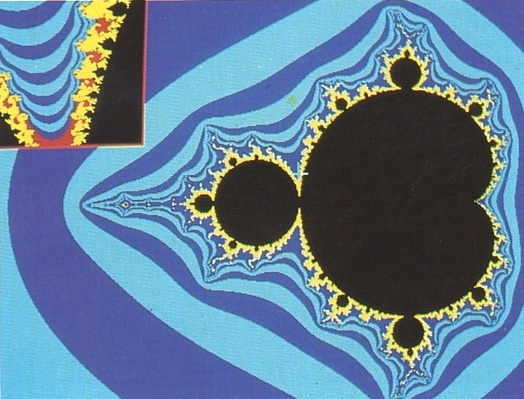
fractal Conjunt de Mandelbrot i un detall (corresponent al punt marcat per una creu blanca) [imatge obtinguda per ordinador al Departament d’Informàtica de la Universitat Autònoma de Barcelona]
Matemàtiques
Model matemàtic o objecte real que manté la seva forma essencial, fragmentada i irregular, tot i variant l’escala d’observació.
Les primeres fractals corbes de Von Koch, Peano, Sierpiński, etc aparegueren entre el 1875 i el 1925 com a contraexemples als intents de formalització de l’actual matemàtica Benoît Mandelbrot, els anys setanta, descobrí que aquests models serveixen per a representar la realitat Basant-se en els conceptes d’homotècia interna i de dimensió en el sentit de Hausdorff-Besikovič 1919, Mandelbrot definí les bases de la geometria fractal, que permet de modelitzar fenòmens com les turbulències, el cabal dels rius, el soroll blanc, la distribució de les galàxies, les estructures geològiques, etc, tots…
recta real
Matemàtiques
Conjunt de tots els nombres reals, juntament amb llur representació en una recta graduada.
Cada representació resta fixada quan damunt una recta gràfica hom ha escollit un origen imatge del nombre zero i una unitat imatge del nombre u Sovint és utilitzat el llenguatge geomètric en parlar dels nombres reals el nombre x és en un entorn del nombre a
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que conté la…
projecció
Matemàtiques
Sistema de representació utilitzat per a obtenir sobre un pla la imatge dels objectes, de manera que a cada punt de la imatge representada, anomenada també projecció, correspongui un punt de l’objecte.
Els principals elements d’una projecció són l' objecte , els raigs projectants , el pla de projecció i la projecció de l’objecte Segons les relacions que guardin entre ells aquests elements, s’originen els diversos sistemes de projecció
immersió
Matemàtiques
Aplicació injectiva d’un conjunt A en un altre B, que conserva les estructures.
L’aplicació f és morfisme si A i B són espais topològics Tota immersió de A dins B permet d’identificar estructuralment A amb la seva imatge