Resultats de la cerca
Es mostren 16 resultats
convergència quadràtica
Matemàtiques
Convergència de variables aleatòries que tenen moment de segon ordre finit ( variància finita: E(|x2|) + ∞) i que és caracteritzada per la distància en mitjana quadràtica .
És a dir, que x n convergeix en mitjana quadràtica a x si d x n , x tendeix a zero quan tendeix a infinit Aquesta convergència implica la convergència en probabilitat, però no la quasi-segura
conjunt inductiu
Matemàtiques
Conjunt X
en el qual si, i només si, ∅ ∈ X
i, per a cada x
∈ X
, el següent x
, x
∪ { x
}, també hi pertany.
L’existència de conjunts inductius cal imposar-la per mitjà de l’axioma de l’infinit El fet que existeixi un conjunt inductiu implica l’existència d’un conjunt inductiu mínim, que és precisament el conjunt ℕ dels nombres naturals
principi de bivalència
Lògica
Matemàtiques
Principi de la lògica de sentències o proposicions, de caire semàntic, que diu: «tota sentència és certa o falsa».
Aquest principi fou enunciat en el cas del càlcul de proposicions, de forma explícita, per primera vegada, a l’escola estoica de Megara lògica i, concretament, per Crisip, si bé ja Aristòtil en De Interpretatione l’havia analitzat i discutit àmpliament Sintàcticament parlant implica les lleis del tercer exclòs, de no-contradicció i de la doble negació, les quals, en lògiques no bivalents, poden esdevenir falses
seminorma
Matemàtiques
Aplicació d’un espai vectorial E en el conjunt de nombres reals positius.
A tot vector x de E assigna un valor ∥ x ∥ de manera que ∥ a x ∥ = | a | ∥ x ∥, i que, per a tot x, y de E , ∥ x + y ∥ ≤∥ x ∥ + ∥ y ∥ Si una seminorma compleix, a més, que ∥ x ∥=0 implica x = 0, aleshores es tracta d’una norma En ℝ 2 el pla, ∥ x , y ∥ = | x + y | és una seminorma que no és norma Tota norma és seminorma, però no inversament
continuïtat uniforme
Matemàtiques
Propietat d’una funció real segons la qual, per a valors pròxims de la variable independent, l’oscil·lació de funció es fa tan petita com hom vulgui.
La funció y = sin x ho és per contra, la y = x 2 no ho és Tota funció uniformement contínua és contínua Formalment f és uniformement contínua si per a tot ε positiu existeix un δ positiu independent dels valors de les variables tal que si / x 1 - x 2 / < δ aleshores / f x 1 - f x 2 / < ε La continuïtat en un interval tancat implica la uniformitat
ordenat | ordenada
Matemàtiques
Dit del conjunt que té definida una relació d’ordre.
Un grup G , + és dit ordenat per la relació d’ordre ≤, si es compleix la propietat d’isotonia o compatibilitat de l’operació + respecte a l’ordre ≤, és a dir, si per tot x, y, z , de G, x ≤ y implica x + z ≤y + z i z + x ≤ z + y Un anell o un espai vectorial són dits ordenats si aquesta llei d’isotonia és vàlida per a totes les operacions que hi són definides
teorema de Gauss
Física
Matemàtiques
Donat un camp vectorial A, per a tota regió de l’espai de volum V limitada per una superfície S, es compleix que: ∫∫sA·dS = ∫∫∫vdivA dV.
El primer terme de l’equació és el flux de A a través de S És anomenat també teorema de la divergència o d’Ostrogadskij En el cas d’un camp elèctric E , el teorema de Gauss pren la forma q essent-hi la càrrega total dins la regió limitada per S, i ε, la constant dialèctica del medi En el cas d’un camp magnètic B , el teorema de Gauss diu cosa que implica la inseparabilitat dels pols magnètics
convergència
Matemàtiques
Qualitat de convergent.
En el cas d’una successió de funcions hom pot parlar de convergència en diferents sentits, segons la topologia donada en el conjunt de funcions a considerar així, hi ha la convergència puntual una successió f n tendeix a f si, per a tot x on les f n estan definides, f n x té límit f x la convergència uniforme f n convergeix uniformement a f si, per a tot ε> 0, es dona un N tal, que n> N implica | f n x - f x |
teoria de les catàstrofes
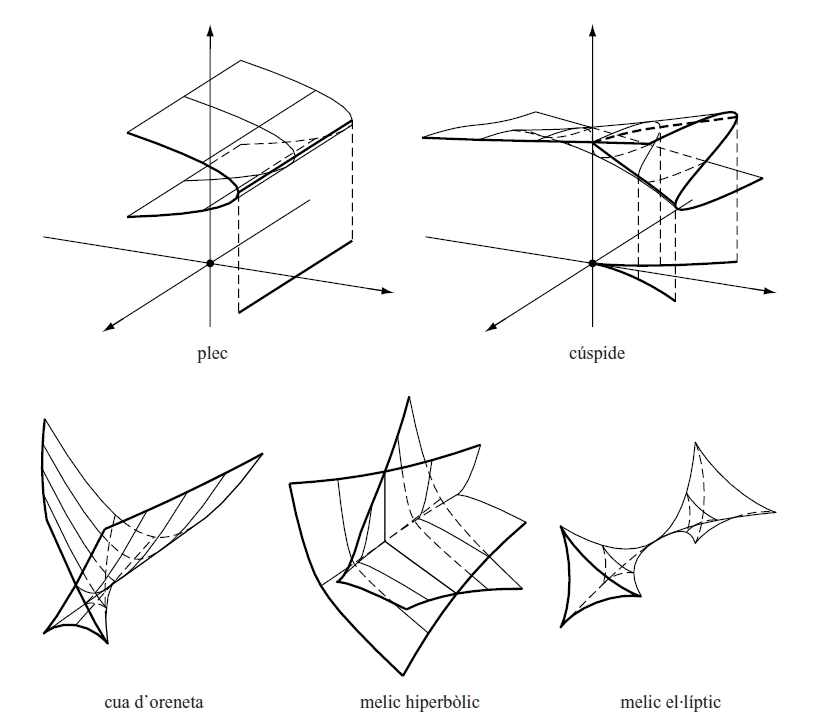
teoria de catàstrofes Les cinc catàstrofes elementals de codimensió menor que quatre
Física
Matemàtiques
Corpus teòric desenvolupat pel matemàtic francès René Thom d’ençà del 1972, i originat en l’intent de modelitzar els canvis discontinus que hom observa en la natura.
En molts sistemes, una petita variació quantitativa de les condicions inicials dóna lloc a una enorme diferència qualitativa en el comportament a llarg termini del sistema situació anomenada bifurcació de comportament Això és important per a l’estudi dels fenòmens d’estabilitat estructural, on cal que el sistema sigui insensible a petites pertorbacions En la teoria de les catàstrofes, aquest requeriment implica que el sistema dinàmic que modelitza el fenomen natural pugui ésser descrit localment per mitjà d’una de les set formes normals conegudes com a catàstrofes elementals , tot i que…