Resultats de la cerca
Es mostren 9 resultats
botella de Klein
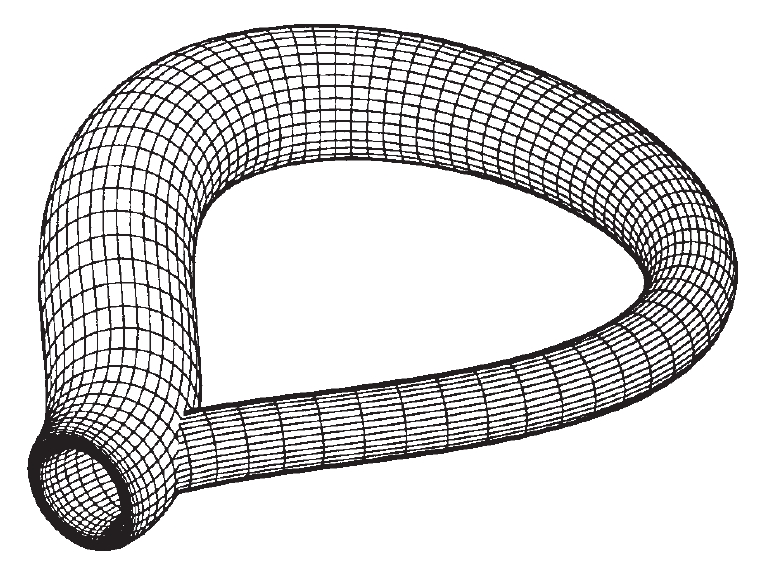
Botella de Klein en una projecció tridimensional
Fototeca.cat
Matemàtiques
Superfície d’una sola cara obtinguda amb una cinta de paper rectangular, formant, primer, un cilindre enganxant dos costats paral·lels i unint, després, els dos cercles que delimiten el cilindre, de manera que mantinguin orientacions oposades.
Sense fer forats és impossible modelitzar a l’espai tridimensional aquesta botella
rectificació
Matemàtiques
Determinació de la longitud d’una corba o d’un arc d’aquesta.
Hom pot provar que la rectificació d’una circumferència és impossible de fer gràficament mitjançant el regle i el compàs
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les…
càlcul numèric
Matemàtiques
Sèrie de mètodes que permet d’obtenir aproximació de les solucions d’un problema matemàtic.
El concepte d’aproximació resta determinat per la natura del conjunt o espai sobre el qual hom calcula i, alhora, per la mètrica o distància definida en ell Donat un espai funcional on hi ha definida una mètrica, aquesta permet de definir una topologia, la qual, a la vegada, ens dóna el concepte de proximitat Un cop fixat l’espai on hom opera i la mètrica que ens definirà la noció d’aproximació, el procés del càlcul numèric es resumeix de la manera següent recull de les dades inicials I del problema dades d’entrada, determinació d’un algorisme de càlcul A , i obtenció de resultats R Aquest…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta de fenòmens…
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per defecte i per excés L’àrea…
probabilitat
Matemàtiques
Concepte que permet d’expressar quantitativament el caràcter aleatori d’un esdeveniment o fenomen que hom creu que pot succeir.
El càlcul de probabilitats , branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s XVII amb els matemàtics B Pascal i P Fermat La motivació principal era l’estudi del guany esperat en els jocs d’atzar ruletes, daus, cartes, etc i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P S Laplace de la següent manera “Si un fenomen pot produir un nombre de resultats diferents i igualment probables,…