Resultats de la cerca
Es mostren 13 resultats
distribució gamma
Matemàtiques
Llei de probabilitat de la variable contínua x, la funció de densitat de la qual és f(x) = e- xxk - 1/Γ(k) (0 < x < ∞;k > 0).
D’aquesta llei deriven algunes expressions particulars, com la llei X 2 i la llei d’Erlang Tendeix cap a la llei normal quan k augmenta indefinidament
funció analítica
Matemàtiques
Funció f:D⊂ℝ→ℝ(o f:D⊂ℂ→ℂ) tal que en tot punt x∈D és desenvolupable en sèrie entera.
Segons que D ⊂ℝo que D ⊂ℂhom parla de funció analítica de variable real o de funció analítica de variable complexa Una funció analítica en D és indefinidament derivable en D
funció tangent
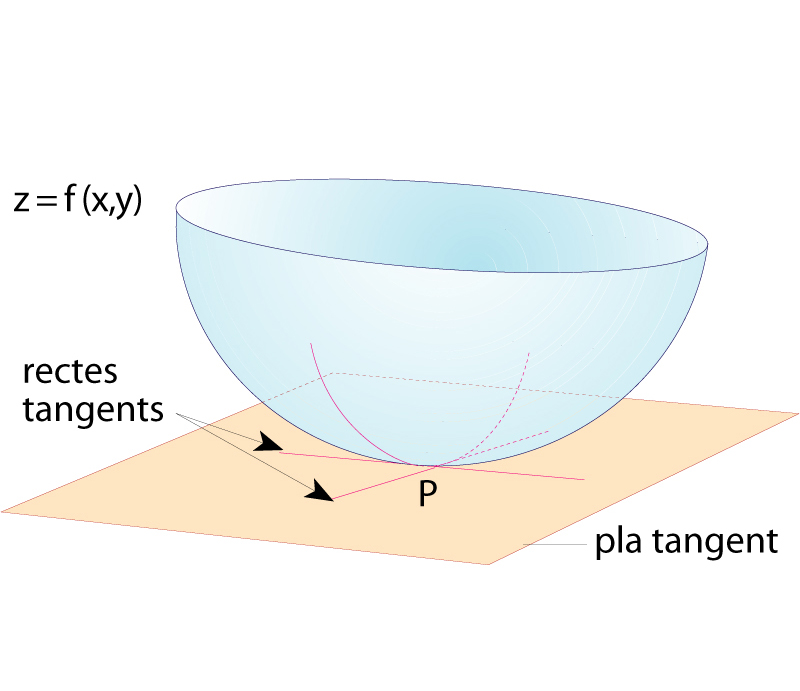
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
postulats d’Euclides
Matemàtiques
Conjunt de cinc principis axiomàtics exposats per Euclides en l’obra Elements, en els quals fonamentà la seva geometria.
Són els següents donats dos punts qualssevol, hom pot traçar una recta que els uneix tota línia recta finita es pot prolongar indefinidament donat un punt qualsevol, hom pot traçar una circumferència amb radi arbitrari i centre en el punt esmentat tots els angles rectes són iguals entre ells i, finalment, donada una recta i un punt exterior, hom només pot traçar per aquest una recta parallela a la recta donada
fracció contínua
Matemàtiques
Expressió de la forma
on l’algorisme s’estén indefinidament.
Hom l’expressa abreujadament mitjançant la notació a 0 + a 1 / b 1 + a 2 / b 2 + a 3 / b 3 + Són emprades per a representar nombres irracionals Així, si α 0 és un nombre irracional positiu, i n ≥0, α 0 admet l’expressió on u n és la part entera de α i α n ≥1 és definit per la relació de recurrència α n - 1 = u n - 1 + 1/α n , n≥1 La successió u n n ≥ 0 és el desenvolupament de α 0 en fracció contínua , i els coeficients u n són els quocients incomplets de la fracció contínua Un exemple d’aquest tipus de desenvolupament és el del nombre π/4, fet per William Brouncker
funció sinus
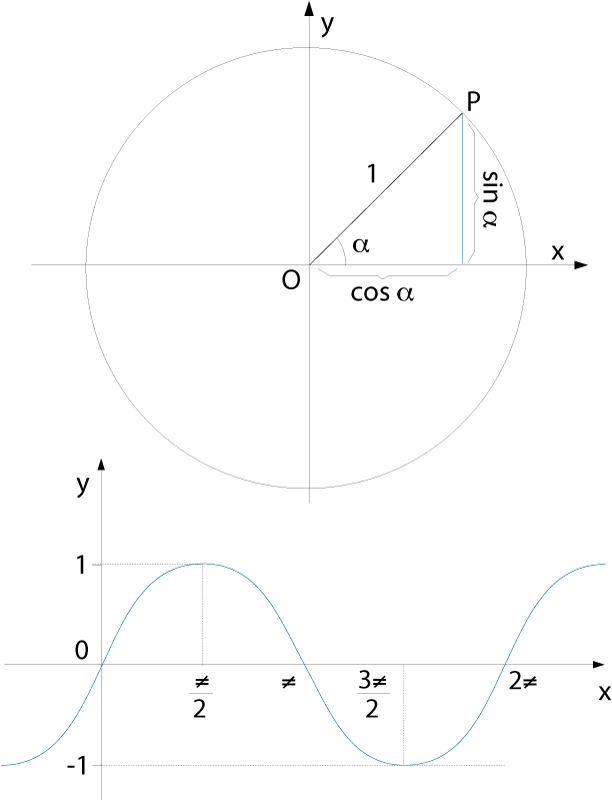
Representació gràfica del sinus d’un angle (a dalt) i de la funció sinus (a baix)
© Fototeca.cat
Matemàtiques
Funció sin: ℝ→ℝdefinida per l’assignació x →sin (x) on sin(x) és el sinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1,1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció cosinus per la derivada d sin x / dx =cos x , d cos x / dx = -sin x És indefinidament derivable i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió sin x= e i x - e i x /2 i , relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció sinus complex
funció cosinus
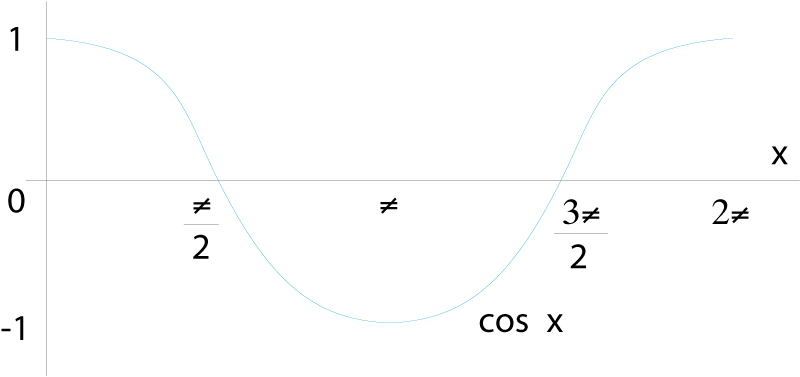
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta…