Resultats de la cerca
Es mostren 14 resultats
funció logarítmica
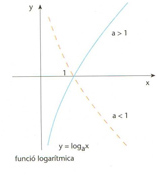
Funció logarítmica
© Fototeca.cat
Matemàtiques
Funció inversa de la funció exponencial
.
És anomenada també funció logaritme Si x = a y , on a > 0 i a ≠1, la funció logarítmica de base a fa l’assignació x → y ≡log a x Hom empra generalment la funció logarítmica de base 10 log 1 0 x i la que té per base el nombre e, o funció logaritme neperià L’extensió al cos ℂés la funció logarítmica complexa
espiral logarítmica
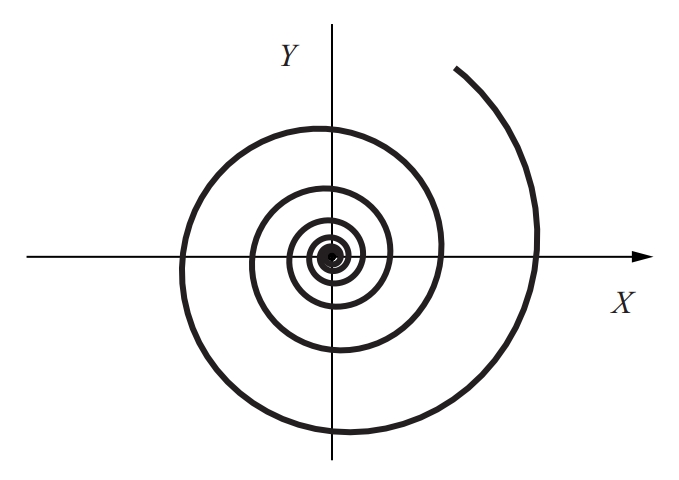
espiral logarítmica
Matemàtiques
Espiral en la qual l’argument és proporcional al logaritme del radi vector, de manera que té com a equació polar r = ekθ, i que talla tots els seus radis vectors segons un mateix angle.
funció logarítmica complexa
Matemàtiques
Funció f:ℂ-{0}→ℂque resulta d’estendre a ℂla funció exponencial.
És definida per l’assignació z →ln z =ln| z |+ i arg z , on | z | és el mòdul de z i arg z el seu argument És la funció inversa de la funció exponencial complexa e l n z =ln e z = z
derivada logarítmica d’una funció en un punt
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt a∈D, derivada de la funció ln|f(x)| en el punt a
.
Així, doncs, la derivada logarítmica de f en a és f´ a / f a
distribució log-normal
Matemàtiques
Distribució de probabilitat d’una variable Y el logaritme de la qual es distribueix de manera normal.
espiral
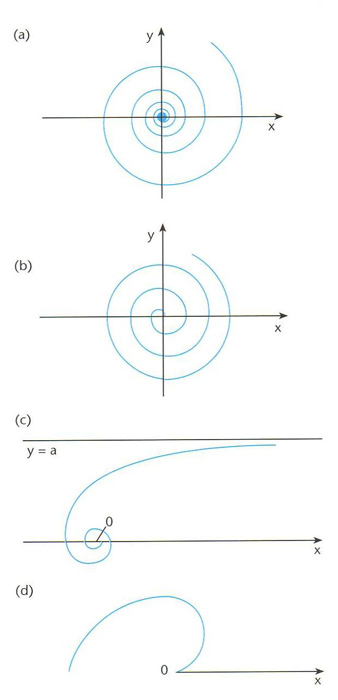
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ
funció exponencial
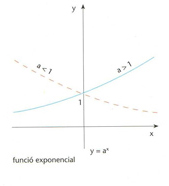
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de…
funció transcendent
Matemàtiques
Funció que no és algèbrica, és a dir que en el seu desenvolupament en sèrie de potències hi ha un nombre infinit de coeficients no nuls.
En són exemples la funció exponencial, la funció logarítmica, i les funcions trigonomètriques o hiperbòliques
funció inversa d’una funció
Matemàtiques
Donada una funció f(x), funció g(x) que satisfà (f₀g) (x)=(g₀f) (x)=x, on ₀és la composició de funcions: (f₀g)(x)=f[g(x)).
La funció inversa de f és representada, generalment, per f - 1 , i hom diu que composta amb f dóna la identitat En són exemples, la funció logarítmica, que és la inversa de la funció exponencial, o la funció arcsinus que és la inversa de la funció sinus
e
Matemàtiques
Nombre irracional i transcendent definit per
.
Els primers coeficients de la seva expressió decimal illimitada són e= 2,7182818284590 És el límit de la sèrie i és relacionat amb els altres nombres fonamentals de la matemàtica per l’expressió e iπ +1 = 0 La funció de ℝen ℝdefinida per x → e x és la funció exponencial,i la definida per és la funció logarítmica , que assigna a cada nombre real el seu logaritme natural o neperià El nombre e i les funcions associades són de gran interès i utilitat en física i matemàtiques