Resultats de la cerca
Es mostren 92 resultats
mètode Simpson
Transports
Matemàtiques
Mètode gràfic de determinació de l’àrea compresa entre una corba i l’eix, aplicable a la determinació del volum comprès entre una superfície corba i un pla, inventat pel matemàtic anglès Thomas Simpson i molt emprat per al càlcul de l’arqueig dels vaixells.
mètode de Montecarlo
Matemàtiques
Mètode estadístic pel qual, mitjançant un mostreig artificial (que en general utilitza successions de xifres aleatòries), hom arriba a estimar la probabilitat que un procés real tingui lloc.
L’ús d’un mostreig artificial o procés de simulació , que actualment és facilitat per la utilització d’ordinadors, evita el mètode analític de comptabilitzar totes les dades reals que concorren en el procés analitzat i que, a causa de llur quantia i aleatorietat, desborden les possibilitats de comptabilització El mètode de Montecarlo fou perfeccionat entre els anys 1950 i 1960, i té com a antecedent històric l’estimació feta per GBuffon, l’any 1773, de les xifres decimals del nombre pi π El mètode ha estat utilitzat amb èxit en física nuclear…
mètode dels mínims quadrats
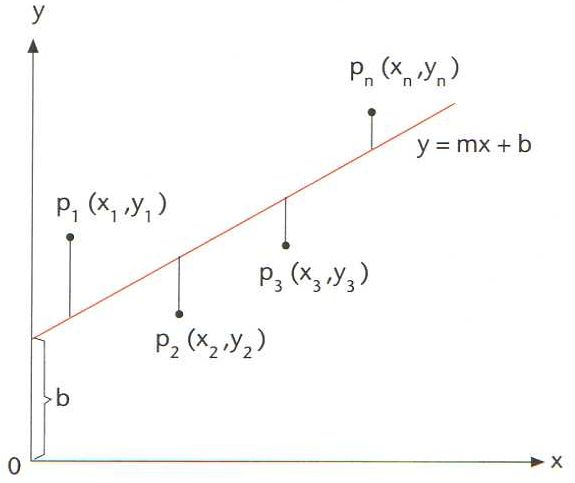
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi de la…
mètode dels elements finits
Matemàtiques
Mètode numèric per a resoldre problemes d’equacions diferencials en derivades parcials.
Matemàticament és una extensió de la tècnica de Rayleigh-Ritz-Galerkin el problema es planteja en forma variacional i hom aproxima la solució mitjançant una combinació lineal de funcions senzilles, en aquest cas funcions polinòmiques a trossos, nulles excepte en un petit domini dintre del qual són polinomis de grau baix El mètode aparegué els anys seixanta entorn de l’aplicació dels ordinadors als càlculs elàstics d’estructures, superà molt de pressa els mètodes de diferències finites i amplià ràpidament el seu camp d’aplicacions i es mostrà molt potent especialment quan la…
mètode de la diagonal
Matemàtiques
Mètode introduït per Cantor per tal d’establir que el conjunt R dels nombres reals no és pas numerable.
Després, però, ha estat usat en molts problemes d’autoreferència
mètode de Smirnov i Kolmogorov
Matemàtiques
Mètode estadístic consistent a arribar a caracteritzar la igualtat de dues poblacions estadístiques mitjançant l’estudi de dues respectives distribucions empíriques, obtingudes en mesurar una mateixa característica en dues mostres d’igual grandària de les respectives poblacions.
NVSmirnov elaborà una teoria matemàtica molt refinada per a deduir la distribució de probabilitats del màxim de les discrepàncies ∣ A t - B t ∣, on A i B són les respectives distribucions empíriques BV Guedenko féu una notòria simplificació d’aquest mètode en traduir el problema a un estudi de trajectòries geomètriques
mètode dels multiplicadors de Lagrange
Matemàtiques
Mètode per a trobar els màxims o mínims d’una funció u = F(x1, x2,..., xn) de n variables, les quals són sotmeses a k condicions suplementàries φ1(x1, x2,..., xn) = 0, φ2(x1, x2,..., xn) = 0,..., φk(x1, x2,..., xn) = 0.
, x n = 0, φ 2 x 1 , x 2 ,, x n = 0,, φ k &x 1 , x 2 ,, x n = 0 El mètode consisteix a formar la funció + λ 2 φ 2 x 1 ,, x n + λ 2 φ 2 > x 1 ,, x n , + + λ k φ k x 1 ,, x n , on λ 1 ,, λ k són constants indeterminades, anomenades multiplicadors de Lagrange les n derivades parcials de ϕ igualades a 0 juntament amb les k condicions constitueixen un sistema de n + k equacions i n + k incògnites λ 1 ,, λ k , x 1 , , x n Atès que aquest sistema constitueix només una condició necessària que la solució del problema ha de satisfer, cal comprovar, un cop resolt el…
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
mètode de les aproximacions successives
Matemàtiques
Procediment de construcció d’un seguit de nombres, an, que s’apropen, a mesura que creix, a un nombre incògnita o que volem determinar.
mètode de reducció a la unitat
Matemàtiques
Mètode que permet de resoldre els problemes de proporcionalitat reduint-los al cas en què la quantitat a què és proporcional la incògnita té el valor de la unitat.
L’aplicació d’aquest mètode a un problema senzill concret és la següent Si sabem que algú recorre 15 km en 3 hores i volem saber quin ha estat el camí recorregut en 2 hores, hom raona així recorre 15/3 km/h = 5 km/h, i, per tant, el camí recorregut en dues hores és 5 x 2 = 10 km El mètode de reducció a la unitat representa una alternativa racional a la regla de tres
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina