Resultats de la cerca
Es mostren 13 resultats
mètode dels mínims quadrats
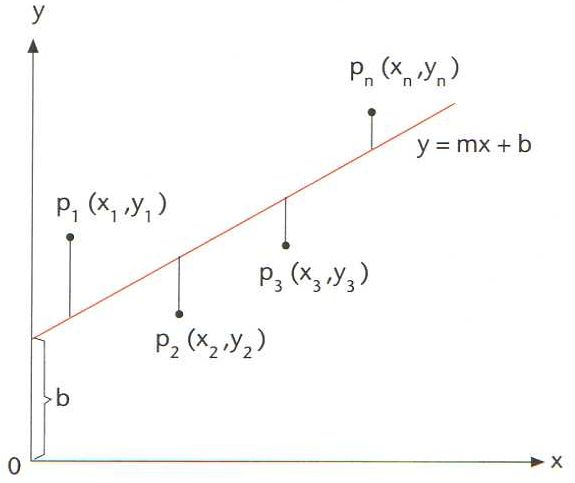
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi…
oval
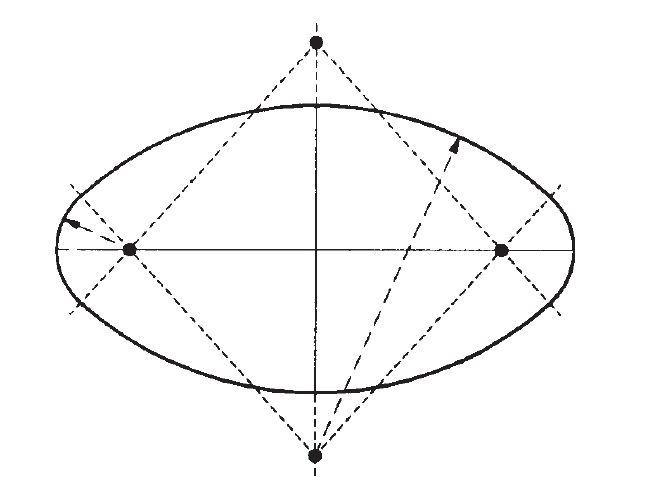
oval
Matemàtiques
Corba amb segona derivada contínua, plana i tancada, en la qual el vector de curvatura és dirigit, en tots els punts, cap a l’interior i, per tant, és completament convexa.
Els punts en què la curvatura passa per màxims i mínims relatius són anomenats vèrtexs de l’oval, i hom demostra que tot oval en té quatre o més Exemples d’oval són les ellipses i el perfil dels ous de gallina
filtratge
Matemàtiques
Mètode numèric per a estimar el valor real d’una magnitud a partir del valor d’una mesura seva.
La diferència entre ambdós valors és anomenada soroll i, per hipòtesi, és una variable aleatòria Entre els mètodes de filtratge hom distingeix els lineals mínims quadrats, mitjanes mòbils i allisatge exponencial i els no lineals mètode de Fourier, de la transformació en z i de Kalman Té aplicació en la predicció i en la previsió
ajust
Matemàtiques
Operació estadística que consisteix a trobar la llei que resumeix, de la millor manera possible, la variació d’una variable aleatòria Y
en funció d’una altra variable X
, de la qual depèn.
Hom fa l’ajust a partir del coneixement de parells de valors x,y obtinguts observant una mostra, com la capacitat pulmonar i l’edat Deixant de banda l’ajust purament gràfic allisatge, habitualment hom pren una funció f x lineal, exponencial, polinòmica, etc i se suposa que y=f x +ε, on ε és un residu aleatori o soroll, i els paràmetres que defineixen la funció són determinats pel mètode dels mínims quadrats
Pierre Simon de Fermat

Retrat de Pierre Simon de Fermat
© Fototeca.cat
Matemàtiques
Història del dret
Advocat occità, sobresortí pels seus treballs matemàtics.
Estudià a Tolosa Introduí per primera vegada l’infinit en el càlcul, descobrí les propietats de diversos nombres i és considerat el creador de la moderna teoria dels nombres Amb Descartes, aplicà l’àlgebra a la geometria, i, amb Pascal, fundà la teoria de les probabilitats Aplicà el concepte de les variables infinitesimals als problemes de quadratura, de càlcul de màxims i mínims i a la construcció de tangents El 1679 el seu fill Samuel escriví Varia opera mathematica , on es recull l’obra de Fermat
mínim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és menor que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també mínim local , i en el cas particular que existeixen les derivades successives de f x es compleix que en el punt a la primera derivada f ' a és nulla i la segona, f ' a , normalment és positiva En el cas, però, que tant f ' a com f ' a siguin nulles, la condició que f x tingui un mínim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i positiva Aquestes són les condicions que hom aplica per a trobar els mínims d’una funció
allisatge
Matemàtiques
Conjunt de mètodes per al tractament de dades estadístiques de tipus cronològic o sèries temporals, que tenen per objecte fer previsions a curt termini basades en les dades anteriors.
Hom tracta de separar la fluctuació aleatòria de la llei subjacent del fenomen, allisant els valors històrics anteriors La més emprada és la tècnica anomenada de les mitjanes mòbils , que pren com a previsió la mitjana aritmètica de les N darreres dades Hom pot veure fàcilment que S t +1 = S t + X t — X t-N /N Si es tracta, p ex, de preveure les vendes d’un producte per al més següent t+ 1, hom pren la mitjana dels darrers dotze mesos, amb la qual cosa hom suposa que s’eliminaran les variacions aleatòries El mètode de l' allisatge exponencial representa una elaboració de l’anterior que…
derivada d’una funció en un punt
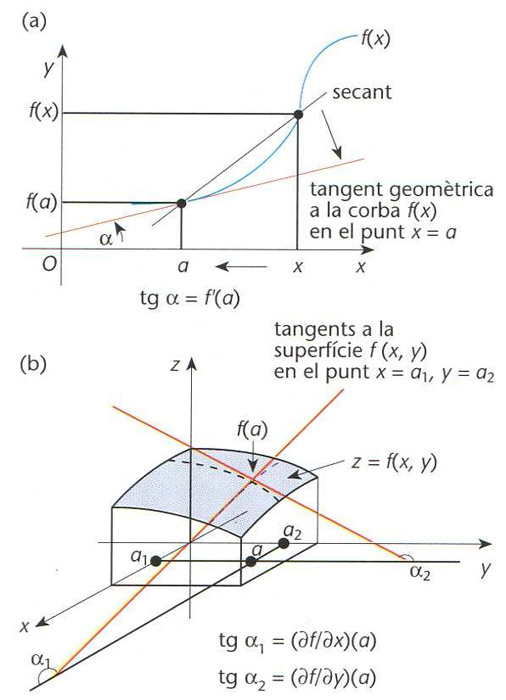
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’ordre…
branca
Matemàtiques
Qualsevol de les parts d’una corba real separada de les altres parts de la corba per discontinuïtats o punts especials (vèrtexs, màxims, mínims, nodes, etc.).
teorema de Bolzano-Weierstrass
Matemàtiques
Teorema emprat en l’estudi de màxims i mínims; afirma que per a una funció y(x) contínua a l’interval tancat [a, b] de la recta, hi ha un valor que és màxim absolut i un altre que és mínim absolut.