Resultats de la cerca
Es mostren 11 resultats
punt asimptòtic
Matemàtiques
Punt singular al qual tendeix una corba donada sense mai abastar-lo.
trocoide
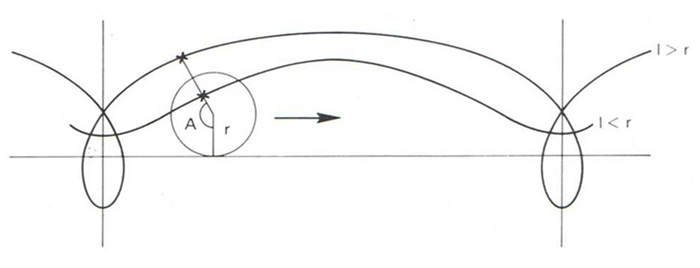
Trociode
© fototeca.cat
Matemàtiques
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
zero
Matemàtiques
Nom de la xifra 0, numeral cardinal que designa l’absència d’unitats.
El zero és l’element neutre en la suma de nombres enters, ja que a + 0 = a , per a tot a Les regles algèbriques del zero són a + 0 = a a 0 = 0 0/ a = 00 si a ≠ 0 0 = 1 Les expressions a /0 i 0/0 són indeterminades ja que 0/0 = 1, car 0 = 1 0, però també 0/0 = 2, car 0 = 2 0, etc, és a dir, que el zero no pot dividir mai El nombre zero i la xifra zero és una creació de la cultura hindú Āryabaṭha, Brāhmagupta, Bhāskara, etc, que cap al segle V dC fou introduït conjuntament amb el sistema decimal de numeració posicional, sistema que els àrabs incorporaren al seu coneixement i…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…
aproximació
Matemàtiques
Ordre de grandor de les desviacions que els valors mesurats o calculats d’una magnitud en un sistema presenten respecte al valor teòric que compliria amb exactitud la llei matemàtica que determina aquest sistema.
El comportament de qualsevol sistema és determinat per unes lleis que es tradueixen en relacions matemàtiques entre les magnituds que defineixen Per exemple, pel corrent elèctric val la llei d’Ohm V = R × I , on V és la tensió aplicada, R la resistència del cos considerat i I la intensitat del corrent en aquestes condicions La validesa d’aquestes lleis significa que, si hom fa mesures independents de cadascuna de les quantitats que hi intervenen V, R i I en l’exemple, els valors obtinguts han de mantenir entre ells la relació matemàtica que expressa la llei del sistema aquest fet, però, no…
Blaise Pascal

Blaise Pascal
Filosofia
Física
Matemàtiques
Matemàtic, físic, filòsof i escriptor francès.
La seva disposició per a les matemàtiques fructificà ja a setze anys amb una notable memòria sobre les corbes còniques, Essai pour les coniques 1640, i poc temps després amb la construcció d’una màquina de calcular que fou l’admiració dels seus contemporanis El gust per les matemàtiques, que mai no l’abandonà, el portà ja cap a la maduresa a estudiar el càlcul de probabilitats, del qual fou, juntament amb Fermat, un dels fundadors Dins el camp de la física, inspirà o bé féu directament nombrosos experiments relatius a la pressió atmosfèrica per exemple, la prova del tub de…
numeració
Matemàtiques
Art d’expressar tots els nombres amb un conjunt finit de mots i de signes.
El sistema de numeració de l’antic Egipte III millenni aC era decimal , o de base 10, és a dir, hom comptava per unitats, desenes, centenes, etc La unitat, la desena, la centena i el miler eren representats, respectivament, amb els símbols ∣, ⋂, ℮, aquest símbols, fins que la suma de valor dels signes escrits era igual al nombre per exemple, el nombre 1235 era ℮℮⋂⋂⋂∣∣∣∣∣ El sistema de numeració babilònic era de base seixanta i ja utilitzava una notació posicional, cosa que suposa la introducció del zero Era, doncs, un sistema essencialment semblant a l’actual, bé que confusionari, puix que,…
cos
Matemàtiques
Conjunt dotat de dues operacions, que hom acostuma a designar + i × (suma i producte), amb les següents propietats: respecte a la suma el conjunt té estructura de grup commutatiu, i també amb el producte és grup, commutatiu o no, i segons això el cos es dirà d’una manera o d’una altra.
A més, hom exigeix que l’operació × tingui la propietat distributiva respecte a la + Hom pot dir, doncs, que un cos és un anell tal, que cada element té invers respecte a l’operació × Un cos té només dos ideals el 0 i ell mateix Els exemples més immediats són el cos ℝdels nombres reals, amb les operacions usuals de suma i producte, el cos ℚdels nombres racionals i el ℂdels complexos Hi ha el cos de dos elements 0 i 1, amb les operacions + 0 element neutre 1 + 1 = 0, i × habitual Com a exemple de cos no commutatiu hi ha el dels quaternions La característica d’un cos és el nombre més petit p…
matemàtica
Matemàtiques
Ciència que estudia les propietats dels nombres, de les figures, dels conjunts, de les operacions, de les funcions, etc.
Aquesta definició és força descriptiva, però incompleta, i per això diversos matemàtics han intentat de definir la matemàtica tot assenyalant-ne els trets més característics Així, segons B Russell, la matemàtica consisteix només en afirmacions tals com “si una proposició és veritable referida a un objecte, aleshores una altra proposició també ho és”, de manera que la matemàtica és aquell camp en què hom no sap mai de què parla ni si allò que diu és veritat o no Dins aquesta mateixa línia, H Poincaré diu que els matemàtics no estudien objectes, sinó relacions entre objectes no els interessa la…