Resultats de la cerca
Es mostren 10 resultats
semblant
Matemàtiques
Dit dels termes algèbrics que contenen les mateixes lletres afectades dels mateixos exponents.
transformada de Carson
Matemàtiques
Funció de la variable complexa p definida per la integral¬66820 ¬en què C f(t) simbolitza la transformada de Carson d’una funció del temps t.
Té les mateixes funcions d’existència que la transformada de Laplace
anell
Matemàtiques
Estructura (A, +, ·) que consta d’un conjunt A en el qual han estat definides dues operacions, l’addició (+) i la multiplicació (·) amb les següents propietats: 1) el conjunt A amb l’operació d’addició és un grup commutatiu; 2) la multiplicació és associativa; 3) la multiplicació és distributiva respecte a l’addició per la dreta i per l’esquerra (és a dir a · (b + c) = a · b + a · c i (a + b) · c = a · c + b · c).
Si l’anell admet element unitat 1 per a la multiplicació a 1 = 1 a = a , aleshores lanell s’anomena anell amb unitat o unitari Cal remarcar que un mateix conjunt pot adquirir estructura d’anell de diverses maneres, canviant la definició de les operacions Exemples Els nombres enters amb l’addició i la multiplicació ordinàries Els nombres parells amb les mateixes operacions Le matrius quadrades amb l’addició i la multiplicació matricials
cercle osculador
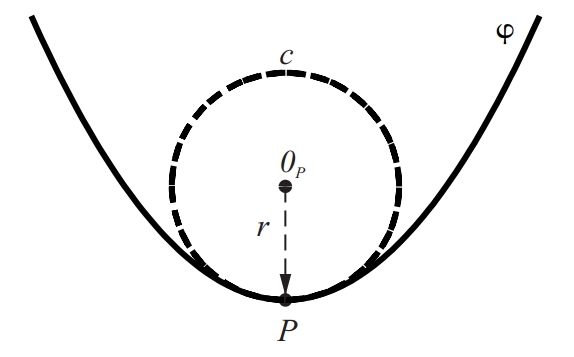
Cercle osculador de la corba φ en el punt P
Matemàtiques
En un punt d’una corba, cercle del pla osculador que té les mateixes tangent i curvatura que la corba en aquest punt.
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que satisfà les mateixes condicions, aleshores existeix una translació T i una…
Bernhard Bolzano
Filosofia
Matemàtiques
Filòsof i matemàtic txec d’origen italià.
Sacerdot catòlic i professor de filosofia de la religió a Praga 1805-20, hagué d’abandonar la càtedra per les seves tendències racionalistes Oposat a l’idealisme kantià, volgué desenvolupar una filosofia científica amb la seva concepció de la lògica com a estudi de les “proposicions com a tals” o en elles mateixes ‘Sätze an sich’ en tant que quelcom objectiu, i amb la seva contribució a la fonamentació de les matemàtiques Féu estudis de les paradoxes de l’infinit descobertes per ell i formulades clàssicament per Georg Cantor Treballà també en funcions reals, convergència de…
Jeroni Munyós
Astronomia
Matemàtiques
Judaisme
Hebraista, astrònom i matemàtic.
Hom ha especulat sobre un possible origen judeoconversEs graduà en arts a València, on estudià vers 1530-40 Professor d’hebreu a la Universitat d’Ancona, tornà a València, on fou professor particular de matemàtiques i catedràtic d’hebreu 1563 i de matemàtiques 1567 de la Universitat El 1579 passà a Salamanca com a catedràtic de les mateixes matèries Observà l’anomenat cometa del 1572 , actualment identificat com a Supernova de Tycho Brahe, sobre el qual publicà Libro del Nuevo Cometa el 1573, des d’on atacà la tradicional creença en la immutabilitat dels astres, en determinà la…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F…
probabilitat
Matemàtiques
Concepte que permet d’expressar quantitativament el caràcter aleatori d’un esdeveniment o fenomen que hom creu que pot succeir.
El càlcul de probabilitats , branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s XVII amb els matemàtics B Pascal i P Fermat La motivació principal era l’estudi del guany esperat en els jocs d’atzar ruletes, daus, cartes, etc i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P S Laplace de la següent manera “Si un fenomen pot produir un nombre de resultats diferents i igualment probables,…