Resultats de la cerca
Es mostren 354 resultats
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…
àlef
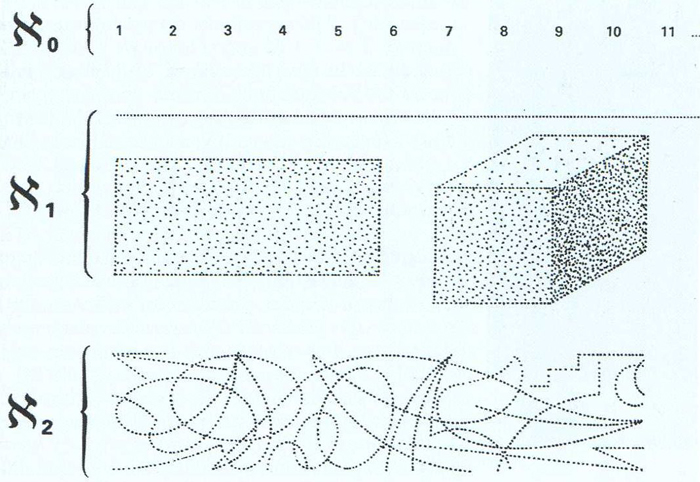
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
políedre
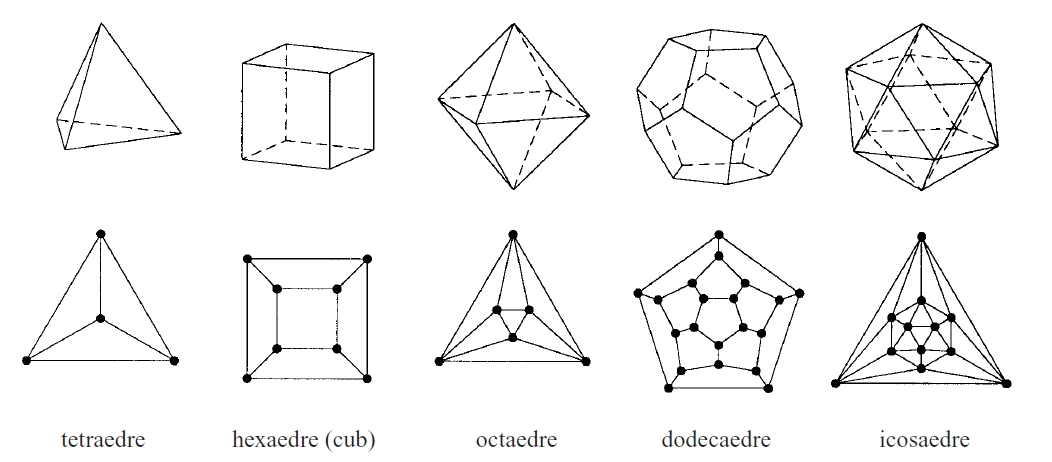
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…
moda
Matemàtiques
Donat un conjunt de dades o observacions, valor de l’observació més freqüent.
És una característica de tendència central Pot donar-se el cas de l’existència de dos o més modes o valors modals en una mateixa distribució
geoplà
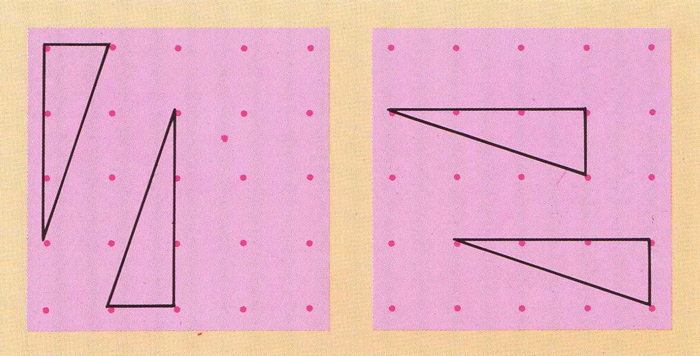
Geoplà
© fototeca.cat
Matemàtiques
Joc didàctic per a estudiar la geometria del pla (en el sentit més ampli).
Consisteix en una taula quadrada on hi ha uns claus o puntes equidistants els més usuals són de 4×4 = 16 o 5×5 = 25 puntes de manera que enganxant-hi unes gomes elàstiques hom pot reproduir figures en diferents posicions per tal d’estudiar-ne propietats geomètriques
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l’estudi del…
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta cadena En el…
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…
nombre enter
Matemàtiques
Nombre que determina quantitats no fraccionables en parts més petites que la unitat.
La manera més simple d’introduir els nombres enters, positius i negatius, és imaginar una escala gràfica en la qual, a partir d’un punt elegit com a origen i designat amb el nombre zero , que no és positiu ni negatiu, hom senyala segments iguals en un sentit i en l’altre, designats amb els nombres naturals successius 1, 2, 3, , als quals hom afegeix, per tal de distingir els sentits, el signe + o el signe - Des d’aquest punt de vista, hom pot dir que un nombre enter és un nombre natural precedit d’un signe +o- Aquesta manera d’introduir els nombres enters, que és molt útil des del punt de…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina