Resultats de la cerca
Es mostren 16 resultats
paràbola
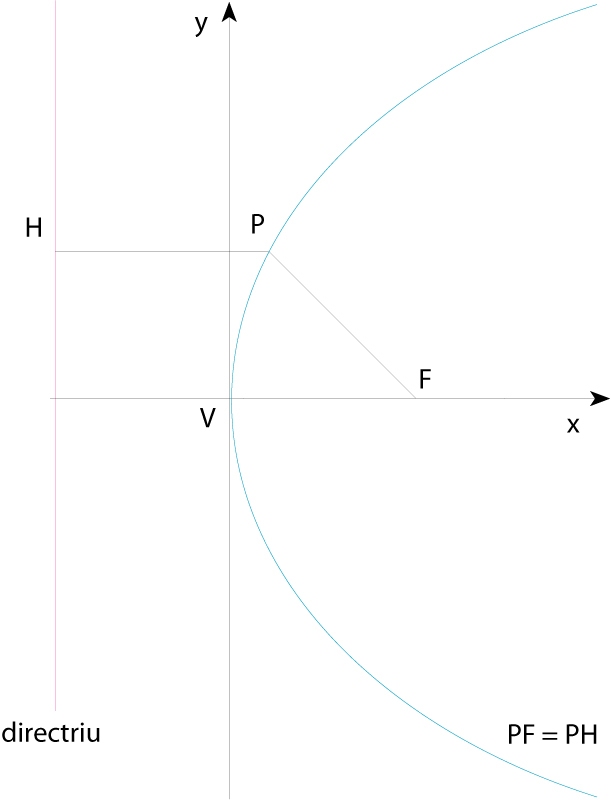
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de…
paraboloide hiperbòlic
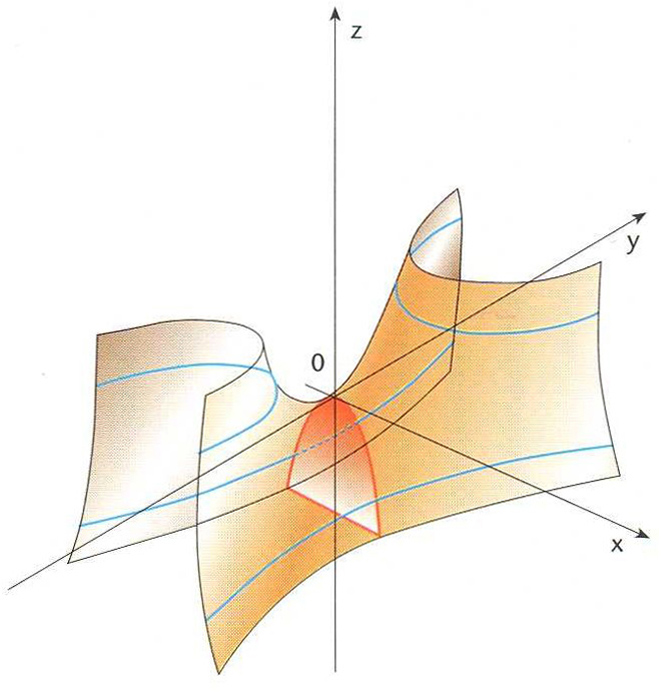
Paraboloide hiperbòlic on hi ha traçada una paràbola i dues hipèrboles
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
—
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola i la intersecció amb un pla perpendicular a l’anterior és una hipèrbola
paraboloide el·líptic
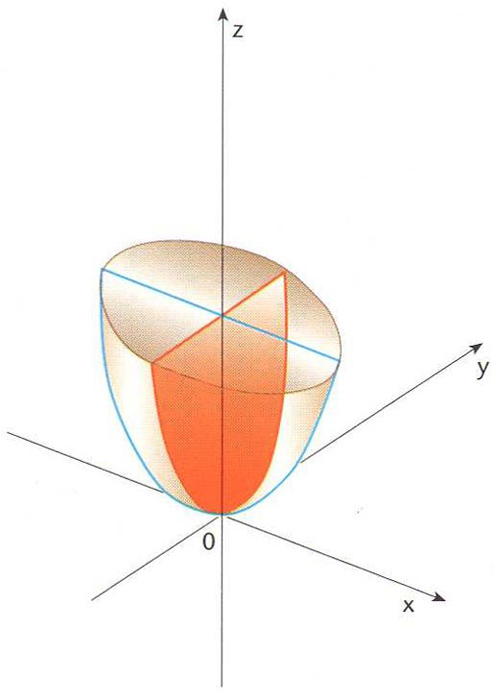
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse
paraboloide de revolució
Matemàtiques
Paraboloide que és generat per una paràbola que gira entorn del seu eix de simetria.
Si p és el paràmetre de la paràbola i l’eix de rotació és l’eix OZ, l’equació és x 2 /p + y 2 /p = 2 z
parabòlic | parabòlica
cònica
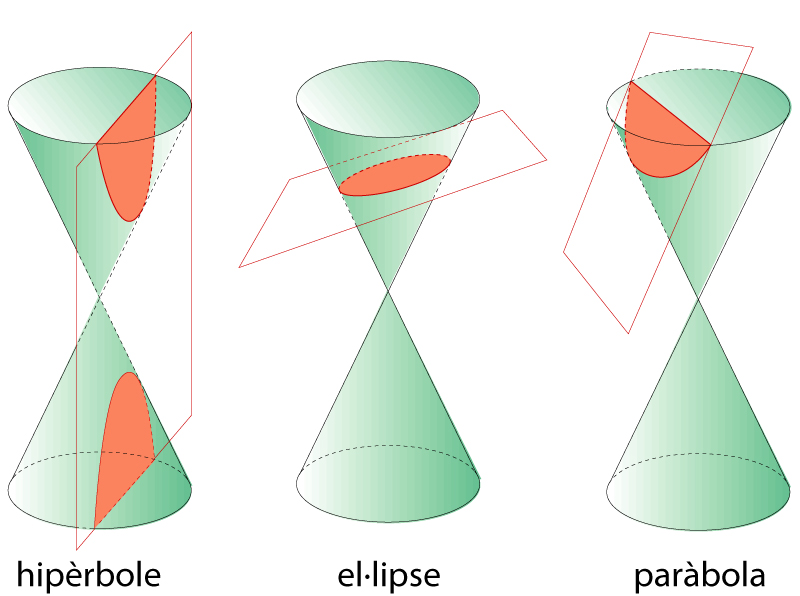
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
directriu d’una cònica
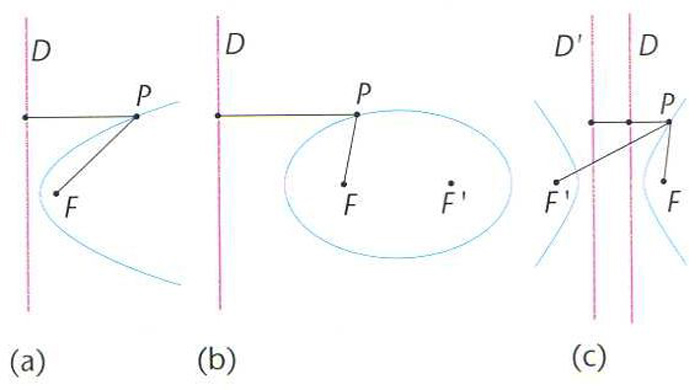
(a) directriu d’una paràbola, PF/PD = 1; (b) directriu d’una el·lipse PF/PDPF/PD = P'F/P'D>1
© fototeca.cat
Matemàtiques
Recta polar d’un focus de la cònica, que permet de definir aquesta com el lloc geomètric dels punts P per als quals el quocient entre la distància del punt al focus PF i la distància perpendicular PD del punt a la directriu és constant.
excentricitat
Matemàtiques
En una cònica, raó entre la distància de qualsevol dels seus punts al focus i la distància perpendicular d’aquest punt a la directriu.
Hom la representa amb la lletra e A la hipèrbola és sempre e > 1, a la paràbola e = 1, a l’ellipse, e < 1 Quan e = 0, l’ellipse degenera en la circumferència
Giulio Carlo del Fagnano
Matemàtiques
Matemàtic italià.
Membre de la Royal Society 1723 Estudià el problema de la rectificació de l’ellipse i la paràbola, i en Opere mathematiche 1711-12 provà que, donada la diferència de longituds de dos arcs, hi havia infinites solucions per a determinar-los sobre aquestes corbes Euler es basà en els seus mètodes per a la demostració del teorema d’addició de les integrals ellíptiques
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla talla un full…