Resultats de la cerca
Es mostren 13 resultats
decil
Matemàtiques
Estadístic d’ordre que té un deu per cent de valors observats més petits que ell.
agrupament de classes
Matemàtiques
Divisió de l’interval que comprèn totes les observacions d’una sèrie estadística en petits intervals iguals.
Cada un d’aquests intervals constitueix una classe, i hom atribueix el valor mitjà de l’interval a totes les observacions que conté El nombre d’observacions dins un interval és anomenat freqüència d’aquest interval
quintil
Matemàtiques
Estadístic d’ordre que té una cinquena part dels valors observats més petits o iguals que ell.
agrupament
Matemàtiques
Divisió de l’interval que comprèn totes les observacions d’una sèrie estadística en petits intervals iguals.
interval
Matemàtiques
Conjunt de nombres més grans o més petits que un nombre real donat: [a,+∞), (a,+∞), (-∞,a] i (-∞,a).
Guillaume de L’Hôpital
Matemàtiques
Matemàtic francès.
Deixeble de Leibniz i de Johann Bernoulli, donà a conèixer el càlcul diferencial i integral inventat per Leibniz i establí la regla que duu el seu nom Amb una prosa elegant i didàctica, escriví Analyse des infiniment petits pour l’intelligence des lignes courbes 1696
anàlisi no estàndard
Matemàtiques
Branca de la lògica matemàtica que fonamenta un càlcul amb infinits i infinitèsims a l’estil de Leibniz.
Hom obté un model no estàndard *R del cos R dels nombres reals com a ultrapotència de R *R és un cos ordenat no arquimedià que conté R i d’altres elements infinitament grans i infinitament petits Per a alguns problemes pot ésser més senzill treballar a *R que no pas a R En tot cas permet una formulació diferent de la pròpia del mètode de Weienstrass amb ε i δ, que pot ésser més intuïtiva Fou desenvolupada per A Robinson a partir del 1960
regla de Simpson
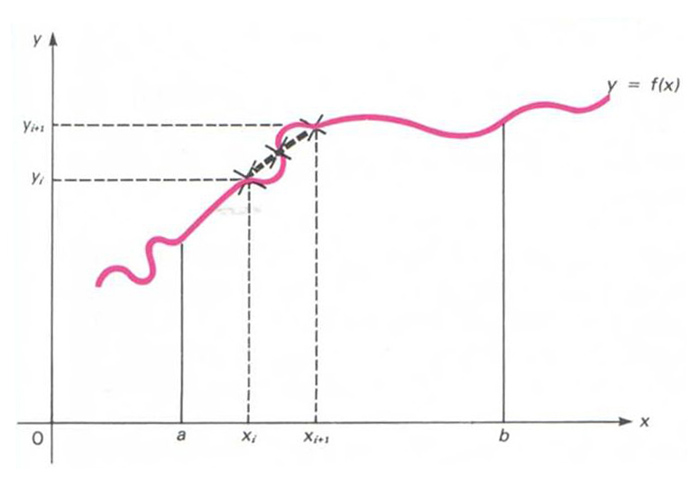
Regla de Simpson
© fototeca.cat
Matemàtiques
Mètode per a aproximar l’àrea limitada per una corba y = f(x), l’eix OX i dues rectes paral·leles x = a i x = b.
El mètode suposa que els petits arcs de la corba són aproximables mitjançant arcs de paràbola que passen pel punt mitjà i pels punts terminals de l’arc considerat La fórmula que hom obté amb aquesta aproximació és usant les sèries de Taylor fins als termes quadràtics on l’interval a,b ha estat dividit en 2 n subintervals a, x 1 , x 2 , , x 2 n - 1 , b , i y a , y 1 , y 2 , , y 2 n - 1 , y b són les respectives ordenades d’aquests punts, y i = f x i La diferència numèrica entre l’àrea real i aquesta àrea aproximativa A , és fitada per la quantitat M b-a 5 /1802 n 2 , on…
papir Rhind

Costat esquerre del dors del papir Rhind
British Museum
Matemàtiques
Papir egipci, que conté un tractat matemàtic, d’època faraònica i en molt bon estat de conservació, que fou adquirit a Tebes l’any 1858 pel viatger britànic A. Henry Rhind i a la seva mort pel British Museum, on és conservat.
Alguns petits fragments del mateix papir foren comprats per Edwin Smith i es troben actualment a la Historical Society de Nova York Data del regnat d’Auserre ApopisI, rei hikse de la dinastia XV ~1674-1567 aC És còpia, però, d’una obra escrita sota Amenemhat III 1842-1797 aC, com indica l’escriba Ahmés en la introducció Comprèn una sèrie de taules per al càlcul de fraccions i noranta problemes aritmètics i geomètrics, la natura dels quals no és teòrica, sinó pràctica càlcul de superfícies, repartiment de béns entre diverses persones, etc Hi són emprats uns algorismes especials de…
definició per recurrència
Matemàtiques
Definició d’una funció sobre els nombres naturals definint-la per a 1 i, per a cada n més gran que 1, en funció dels valors que pren per a nombres més petits que n
.
Per exemple, la funció factorial pot ésser definida fent 1 = 1 i, per a un n > 1, fent n = n -1 n Aquests procediments de demostració i de definició, ja coneguts i emprats pels grecs, han estat generalitzats i ara hom utilitza les recurrències a qualsevol conjunt ben ordenat on tot subconjunt té mínim Aleshores, per a demostrar que una proposició és veritable per a tot element del conjunt ben ordenat, basta demostrar que és veritable per a tot element si ja ho és per a tots els anteriors