Resultats de la cerca
Es mostren 19 resultats
políedre
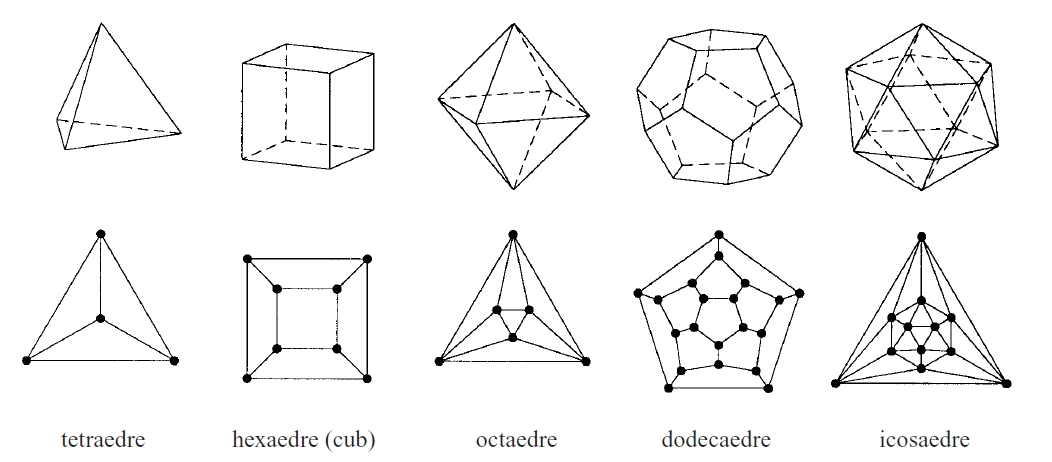
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’…
semblant
Matemàtiques
Dit dels polígons que, tenint angles iguals, tenen costats proporcionals.
Zenodor
Matemàtiques
Matemàtic grec de l’escola d’Alexandria.
Comparà les superfícies dels polígons isoperímetres i arribà a la conclusió que el cercle és el que enclou l’àrea màxima arribà també a una conclusió anàloga pel que fa a l’esfera
polítop
Matemàtiques
Conjunt de punts de l’espai ℝn limitat per hiperplans.
La noció de politop generalitza la de polígon i la de políedre De fet, els politops de ℝ 2 són els polígons i els politops de ℝ 3 són els políedres Un exemple de politop a ℝ 4 és el tesseractis , que és l' hipercub de quatre dimensions
mosaic
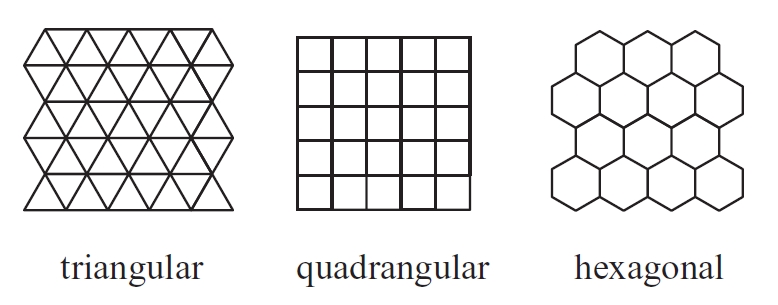
mosaics
© Fototeca.cat
Matemàtiques
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
centroide
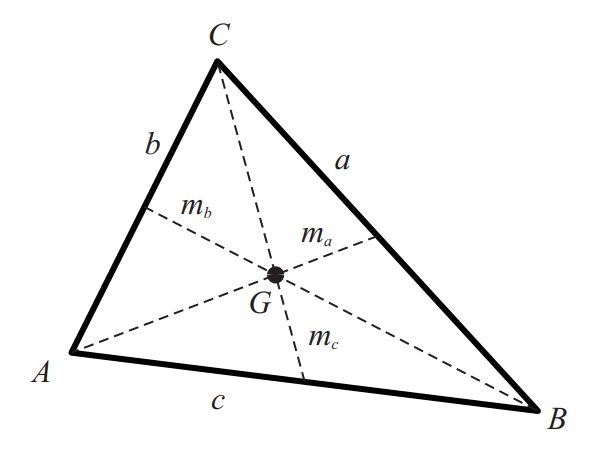
del triangle ABC
Física
Matemàtiques
Punt especial associat a una figura o a una distribució de punts que en el cas físic correspon al centre de massa o de gravetat, de vegades anomenat també baricentre.
En algunes figures el seu centroide és determinat geomètricament Per exemple, en un triangle és el punt d’intersecció de les mitjanes, i en els polígons políedres regulars és el centre de la circumferència esfera circumscrita Donat un conjunt discret de punts x 1 ,, x n amb masses m 1 ,, m n , punt que té per coordenades la mitjana de les coordenades dels punts ponderada per les masses En altres figures es poden trobar per integració les expressions de les coordenades del centroide Així, en figures amb una distribució de massa contínua φ x , el centroide és el punt x̄ = ƒφ x xdx…
pi
Matemàtiques
Lletra grega adoptada per a representar la raó constant que hi ha entre la longitud de la circumferència i el seu diàmetre: 3,141592....
Les fórmules de càlcul són longitud de la circumferència, 2πR àrea del cercle, πR 2 àrea de l’esfera, 4πR 2 volum de l’esfera, Pi és inicial del mot grec περιφέρεια ‘circumferència’ L’ús d’aquesta lletra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al segle XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum el mateix Euler i J Bernoulli usaren P i c , respectivament, com a símbol representatiu A Egipte s'havien fet aproximacions empíriques del valor de π Fou Arquimedes qui…
prisma

Elements d’un prisma (a l’esquerra) i prisma triangular recte (a la dreta)
© Fototeca.cat
Matemàtiques
Políedre que té dues cares iguals i paral·leles (dites bases), les altres cares (dites cares laterals) essent paral·lelograms.
Les interseccions entre les cares laterals són les arestes laterals Una diagonal és una recta que uneix dos vèrtexs qualssevol, que no són de la mateixa base L’ alçada és la distància perpendicular entre les dues bases L’ àrea lateral és la suma de les àrees de les cares laterals l’ àrea total és l’àrea lateral més l’àrea de les bases, i el volum és el producte de l’àrea d’una base per l’altitud Un prisma és anomenat triangular, quadrangular, pentagonal , etc, si les bases són, respectivament, triangles, quadrilàters, pentàgons, etc Un prisma és anomenat recte si les bases són perpendiculars…
número d’or
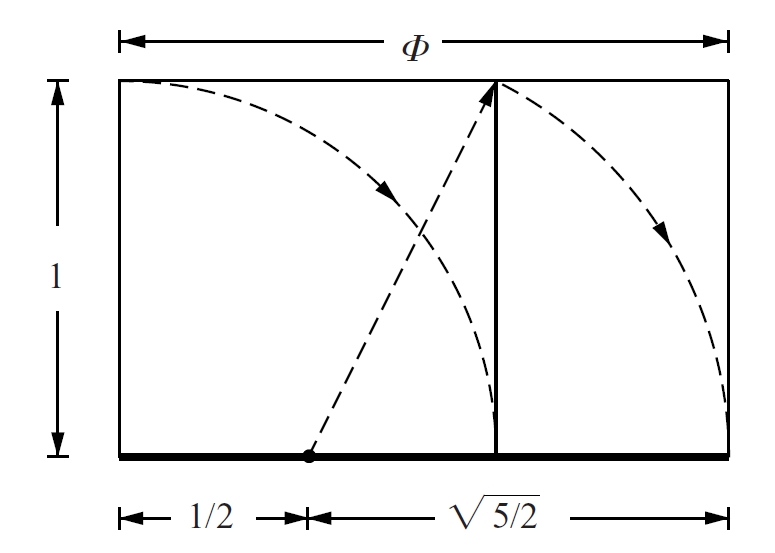
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant, està lligat…