Resultats de la cerca
Es mostren 20 resultats
sèrie de potències
Matemàtiques
Donada una funció real de variable real f (x) derivable indefinidament en el punt x0, sèrie Σ an (x-x0)n amb an = (1/ n !) fn (x0).
Es compleix que f x = Σ a n x- x 0 n per a tots els punts x tals que | x- x 0 | < R, on R és el radi de convergència de la sèrie Aquesta sèrie és anomenada sèrie que desenvolupa la funció f en un entorn del punt x 0 , o sèrie de Taylor de f en el punt x 0 La sèrie de potències és utilitzada per a expressar el desenvolupament en sèrie d’una funció Així, per exemple, hom té la sèrie exponencial , que és convergent per a tot x
desenvolupament en sèrie
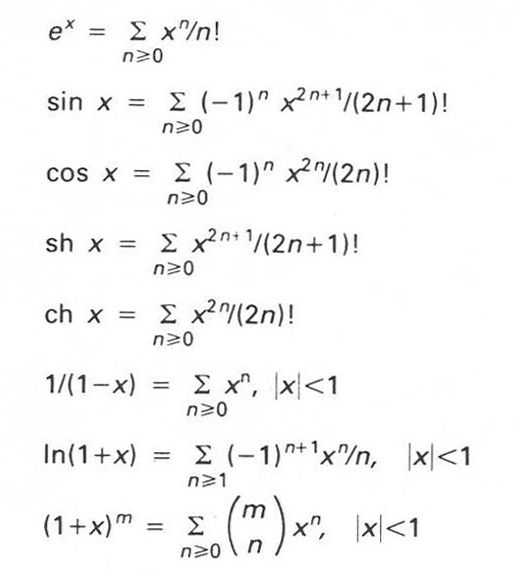
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
analític | analítica
funicó holomorfa
Matemàtiques
Funció de variable complexa si és diferenciable en tots els punts del seu domini.
De fet, coincideixen amb les analítiques, que són les funcions desenvolupables en sèrie de potències d’exponents sencers
submúltiple
Matemàtiques
Donat un nombre enter n, nombre m tal, que m = n/a, on a és també enter.
Una definició anàloga pot ésser feta per a polinomis Els submúltiples decimals d’una quantitat són les quantitats que resulten de multiplicar-la per potències negatives de deu
sistema binari
Matemàtiques
Electrònica i informàtica
Sistema de numeració de base dos.
En aquest sistema hom només necessita dos signes que representin els nombres zero i u Qualsevol nombre natural pot ésser descompost en suma de potències de 2, i el nombre resta determinat dient quines potències entren en la descomposició indicades amb el coeficient 0 o 1 Així, el nombre 45 = 2 5 + 2 3 + 2 2 + 2 0 és escrit, en sistema binari , 101101 dos Per a passar un nombre donat en el sistema binari al sistema decimal cal tenir en compte que cada unitat en val dues de l’ordre immediat inferior Així, el nombre 1010111 dos és Hom pot també representar, en el…
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
nombres de Bernoulli
Matemàtiques
Nombres racionals Bn que apareixen com a coeficients dels termes, per a n parell de la forma
en el desenvolupament en sèrie de potències de la funció Així, B 1 = 1/6, B 2 = -1/30, B 3 = 1/42, etc Alguns autors anomenen nombres de Bernoulli els coeficients B n de x n / n en el desenvolupament de MacLaurin de x / e x -1, de què resulta B 0 = 1, B 1 = -1/2, B 2 = 1/6, B 4 = -1/30, B 6 =1/92, … i B 2 n +1 =0 Hom empra els nombres de Bernoulli en fórmules d' integració numèrica i en càlcul de diferències finites
potència
Matemàtiques
Donats un nombre a
, anomenat base
, i un nombre natural n
, anomenat exponent
, producte
a n
de n
factors iguals a a
, és a dir,
.
Hom generalitza la noció de potència al cas en què l’exponent és un enter negatiu, mitjançant la fórmula a -n =1/a n , i al cas en què l’exponent és un nombre racional, mitjançant la fórmula La generalització al cas que l’exponent sigui un nombre real qualsevol té lloc mitjançant la funció exponencial , i en el cas que l’exponent sigui un nombre complex, mitjançant la fórmula de De Moivre Les propietats més importants de les potències són
funció generatriu d’un conjunt de funcions
Matemàtiques
Funció de dues variables f
( z,u
) tal que el seu desenvolupament en sèrie de potències respecte a una de les variables, p ex u
, té com a coeficients d’aquestes potències les funcions del conjunt en qüestió.
Així, la funció és la funció generatriu de les funcions de Bessel d’índex enter, J n z