Resultats de la cerca
Es mostren 20 resultats
regla de L’Hôpital
Matemàtiques
Regla que permet de calcular límits de funcions en el cas d’indeterminacions del tipus 0/0 o ∞/∞.
Segons aquesta regla, el límit del quocient de dues funcions és igual al quocient de llurs derivades, o sia Si el quocient entre les primeres derivades continua essent indeterminat, hom aplica la regla prenent les segones derivades, i així successivament, fins a resoldre la indeterminació
anàlisi factorial
Psicologia
Matemàtiques
Tècnica estadística que descriu i explica les relacions entre unes variables aleatòries, directament observables, i unes altres de latents, també aleatòries, anomenades factors, que poden ser causa de les primeres.
D’ús freqüent en la investigació experimental psicològica i pedagògica, és basada en la teoria de les correlacions i té per objecte de manifestar el grau de variabilitat comuna existent en un cert camp de fenòmens cada una de les dimensions d’aquesta variabilitat és anomenada factor, i n'existeixen de diversos ordres entre ells cal diferenciar els comuns i els específics S'aplica, sobretot, en l’estudi de les diferències individuals i en la indagació de les aptituds i les qualitats de la personalitat L’iniciador fou Charles Spearman, el 1904, amb la teoria bifactorial, i un dels més grans…
triangle de Tartaglia
Matemàtiques
Disposició triangular de nombres enters que en línia horitzontal dóna ordenadament els coeficients de la potència n-èsima del binomi (a+b).
Establertes les dues primeres línies, les successives són obtingudes collocant la unitat com a primer i últim element, i com a elements intermedis els nombres resultants de la suma dels dos elements contigus de la fila anterior El triangle de Tartaglia és anomenat també triangle de Pascal
matriu wronskiana (de n funcions)
Matemàtiques
Donades n funcions d’una variable real, f1,...,fn, matriu que té a la primera fila les funcions donades, i a les (n—1) files restants, les (n—1) primeres derivades: .
Rep el seu nom del matemàtic J M H Wroński
teorema de Schwarz
Matemàtiques
Teorema referit a una funció real f de dues variables reals, f: ℝ2 → ℝ.
Afirma que si existeixen les derivades primeres ∂ f /∂ x i ∂ f /∂ y en un entorn U d’un punt x 0 , y 0 , i existeix la derivada segona ∂ 2 f /∂i> x∂ y i és contínua en el punt x 0 , y 0 , aleshores existeix la derivada segona ∂ 2 f /∂ y ∂ x al punt x 0 , y 0 i se satisfà que ∂ 2 f /∂ x ∂ y x 0 y 0 = ∂ 2 f / ∂ y ∂ x x 0 , y 0 El teorema de Schwarz és una simplificació del teorema de Bonnet
fractal
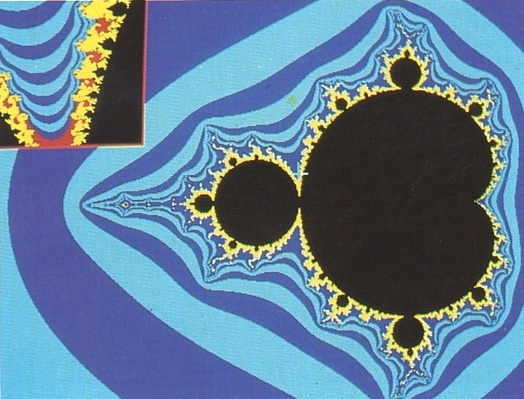
fractal Conjunt de Mandelbrot i un detall (corresponent al punt marcat per una creu blanca) [imatge obtinguda per ordinador al Departament d’Informàtica de la Universitat Autònoma de Barcelona]
Matemàtiques
Model matemàtic o objecte real que manté la seva forma essencial, fragmentada i irregular, tot i variant l’escala d’observació.
Les primeres fractals corbes de Von Koch, Peano, Sierpiński, etc aparegueren entre el 1875 i el 1925 com a contraexemples als intents de formalització de l’actual matemàtica Benoît Mandelbrot, els anys setanta, descobrí que aquests models serveixen per a representar la realitat Basant-se en els conceptes d’homotècia interna i de dimensió en el sentit de Hausdorff-Besikovič 1919, Mandelbrot definí les bases de la geometria fractal, que permet de modelitzar fenòmens com les turbulències, el cabal dels rius, el soroll blanc, la distribució de les galàxies, les estructures…
Jakob Bernoulli
Matemàtiques
Matemàtic suís.
Després d’estudiar teologia s’inicià en matemàtiques i astronomia, i a partir dels estudis sobre el càlcul de Leibniz començà a treballar sobre sèries numèriques, que el portaren a aconseguir les primeres avaluacions asimptòtiques Proposà el problema de la catenària i, en intentar de resoldre el problema de la braquistòcrona , n'obtingué la solució amb mètodes que contenien el càlcul de variacions, que desenvolupà en l’obra Analysis Magni Problematis Isoperimetrici 1701, on inclogué la primera integració d’una equació diferencial A l' Ars conjectandi enuncià l’anomenat teorema de…
anàlisi factorial
Matemàtiques
Tècnica estadística que tracta de descriure i explicar les relacions entre unes variables aleatòries directament observables i unes altres de latents també aleatòries, anomenades factors, i que poden ésser la causa de les primeres.
Gairebé tots els models suposen relacions lineals entre ambdues classes variables Hom acostuma a fer l’anàlisi partint d’un nombre molt gran d’observacions per tal d’obtenir estimacions d’una gran precisió, per a cadascuna de les quals hom tindrà un conjunt de resultats que formen la matriu de les dades Mitjançant aquesta matriu hom calcula els coeficients d’intercorrelació entre les variables i després, mitjançant els mètodes del model factorial emprat, les saturacions de les variables en els factors comuns i les comunitats de cada variable, equivalents a la correlació de cada variable amb…
Maryam Mirzakhani

Maryam Mirzakhani
© Stanford University
Matemàtiques
Matemàtica iraniana.
El 1994 i el 1995 guanyà les medalles d’Or de les Olimpíades Internacionals de Matemàtiques per a estudiants no universitaris El 1999 es graduà a la Universitat Tecnològica de Sharif Teheran i posteriorment ingressà a la Universitat de Harvard, on preparà la tesi doctoral amb Curtius McCullen 2004 En 2004-08 treballà al Clay Mathematics Institute i fou professora a la Universitat de Princeton Aquest darrer any s’incorporà com a docent a la Universitat de Stanford El seu camp d’estudi se centrà en la topologia de dimensió baixa, i una de les…
Josep de Saragossa i Vilanova
Astronomia
Matemàtiques
Matemàtic i astrònom.
Mestre en arts a la Universitat de València, interessat des de jove per les matemàtiques, no acceptà una càtedra a la universitat per professar a la Companyia de Jesús Residí en diverses ciutats, fou professor al collegi de l’orde a Mallorca, on estigué en contacte amb l’historiador i matemàtic Vicent Mut Ensenyà després a Barcelona, i el 1660 passà al collegi de Sant Pau de València, on es dedicà a l’estudi i l’ensenyament de matemàtiques i a l’observació astronòmica El 1670 fou nomenat titular de la càtedra de matemàtiques del collegi de Sant Isidre de Madrid, on restà els darrers anys de…