Resultats de la cerca
Es mostren 31 resultats
autòmat finit determinista
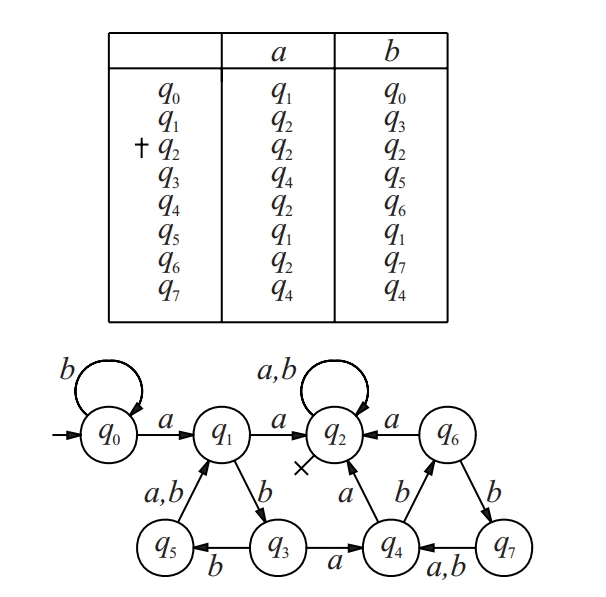
autòmat finit determinista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
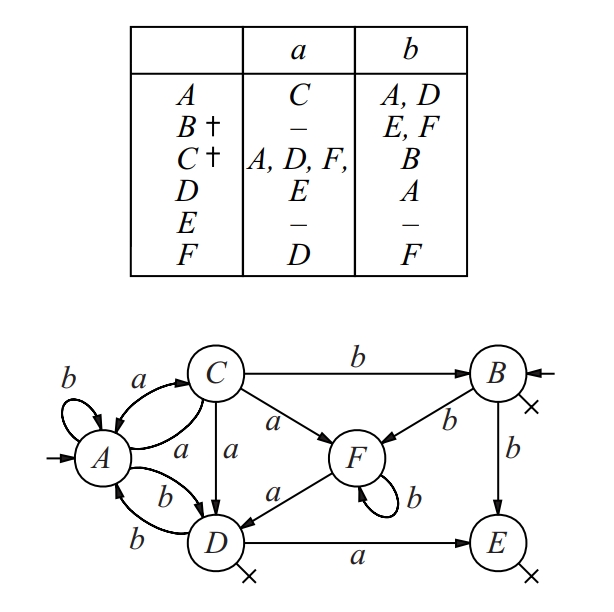
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
lleis de De Morgan
Lògica
Matemàtiques
En lògica d’enunciats, lleis donades per les equivalències següents: no(P i Q) = (no P) o (no Q), i no(P o Q) = (no P) i (no Q).
En teoria de conjunts, lleis donades per les igualtats i on les barreres indiquen els conjunts complementaris Les lleis de De Morgan se satisfan en tota Boole, àlgebra de
àlgebra tensorial
Matemàtiques
És, dins de l’àlgebra abstracta, una construcció d’una àlgebra associativa T(E) partint d’un espai vectorial V.
Sigui E un espai vectorial sobre un cos commutatiu K , per a cada parella p , q de nombres naturals, existeix una aplicació bilineal única T pq de T p E X T q E en T p+q E tal que, per a tot element x 1 ,, x p d’ E p i tot element x p+1 ,, x p+q d’ E q , T pq x 1 OOOoooOOO x p , x p+1 OOOoooOOO x p + q = x 1 OOOoooOOO x p+q , on T n E és la potència tensorial n -èsima d E Les aplicacions bilineals T pq defineixen sobre l’espai vectorial una estructura de K -àlgebra graduada És l’àlgebra…
producte tensorial
Matemàtiques
Aplicació definida entre dues aplicacions multilineals.
Donades dues aplicacions multilineals, f E 1 x E 2 xx E p → K i g F 1 x F 2 xx F q → K , aplicació f ⊗ g E 1 xx E p x F 1 xx F q → K que és definida per l’assignació f ⊗ g x 1 ,, x p , y 1 ,, y q = f x 1 ,, x p g y 1 ,, y q Si els espais E i i F j són de dimensió finita, la matriu associada a f⊗g és anomenada matriu producte tensorial de les matrius associades a f i g
àlgebra graduada
Matemàtiques
Àlgebra sobre un cos, altrament conegut com R-àlgebra, en la qual hi ha una noció consistent del pes d’un element. La idea és que els pesos dels elements se sumin quan es multipliquen els elements tot i que ha de permetre l’addició ‘inconsistent’ de diversos pesos.
Àlgebra E sobre un cos commutatiu K que és suma directa d’una successió de subespais { E n n ∈ ℕ } i, per a cada parella p , q de nombres naturals, el producte d’un element d’ E p per un element d’ E q pertany a E p+q
màquina de Turing
Matemàtiques
Màquina formada per una cinta il·limitada, dividida en cel·les, i per una capsa negra amb un cap lector.
Procedeix de la següent manera elemental A cada cella de la cinta hom pot escriure un 0 o un 1 Aleshores, la màquina de Turing, segons l’estat intern de la capsa negra i del símbol que llegeix el cap lector, pot pendre una de les cinc decisions següents 1, escriure un zero a la cella llegida pel cap lector, esborrant abans el que pugui haver-hi escrit 2, escriure un 1 a la cella, esborrant abans el que pugui haver-hi escrit 3, donar un pas cap a la dreta 4, donar un pas cap a l’esquerra 5, aturar-se Una màquina de Turing és, doncs, una matriu com ara Aquesta matriu actua de la forma següent…
varietat diferenciable
Matemàtiques
Espai topològic separat V en el qual hi ha definida una família de funcions reals ℱ = ℱ(V).
Aquestes funcions reals compleixen les següents condicions si f és una funció V → ℝ tal, que per a tot punt p de V existeix una funció q de ℱ que coincideix amb en un cert entorn de p , aleshores f és de ℱ si f 1 , , f K són funcions de ℱ, i si F és una funció diferenciable qualsevol sobre l’espai euclidià ℝ k , aleshores F f 1 , , f n pertany a ℱ per a tot punt p de V existeixen funcions f 1 , , f n de F tals, que l’aplicació q → f 1 q , , f n q dóna un homeomorfisme entre un cert entorn U de p un obert de ℝ n Tota funció f de…
parell de nombres primers bessons
Matemàtiques
Parell (p,q) de nombres primers, en el qual q=p+2, p ex (5,7), (17,19).
Hom desconeix si llur nombre total és finit, però si sabem que la sèrie , on p recorre els nombres primers bessons, és convergent teorema de Brun
C
Matemàtiques
Cpq designa el nombre de combinacions d’ordre q, formades a partir de p elements.