Resultats de la cerca
Es mostren 21 resultats
mètode dels mínims quadrats
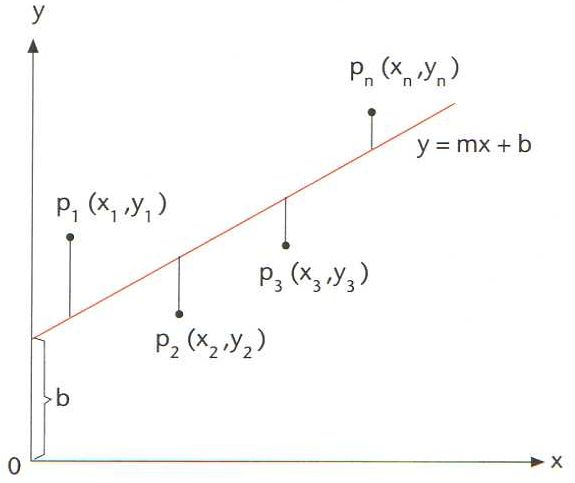
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat…
teorema d’Apol·loni
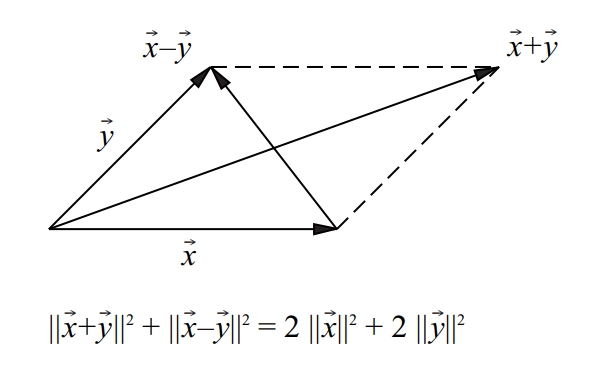
Formulació vectorial del teorema d’Apol·loni
Matemàtiques
Teorema de geomètria mètrica segons el qual en tot triangle la suma dels quadrats de dos costats és igual al doble de la suma del quadrat de la meitat del tercer costat més el quadrat de la mitjana corresponent a aquest darrer costat.
En la seva formulació actual, amb vectors i normes, aquest teorema s’anomena també llei del parallelogram i estableix que la suma dels quadrats de les dues diagonals del parallelogram és igual a la suma dels quadrats dels quatre costats
regressió
Matemàtiques
Estudi de la millor aproximació d’una variable estadística y a partir d’una família donada de variables estadístiques x1..., xn, mitjançant combinacions lineals del tipus a1 x1..., an xn + b, i prenent com a criteri de “millor aproximació” el del mètode dels mínims quadrats.
Dit d’una altra manera, cal cercar els anomenats coeficients de regressió a 1 , a 2 , , a n , b , tals que facin mínima la distància al quadrat d 2 y, a 1 x 1 + + a n x n +b Si hom representa els valors de les variables estadístiques en l’espai ℝ n + 1 , aleshores l’hiperplà y = a 1 x 1 + + a n x n + b és dit de regressió per a n = 1, hom té la recta de regressió , i per a n = 2, el pla de regressió En el cas que n = 1, la recta de regressió y = ax + b té per coeficients on x i , y i són els valors de les variables, i x, y , les seves esperances o valors mitjans En el núvol de…
corba de Peano
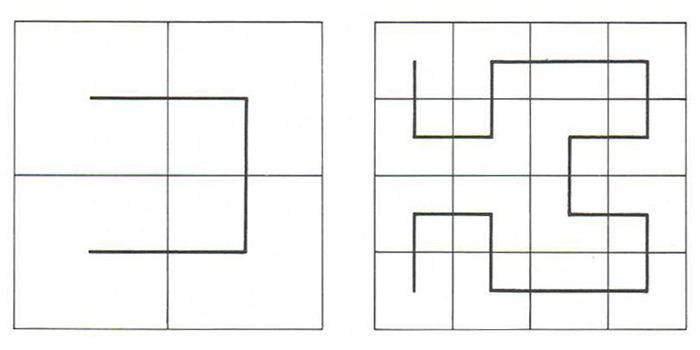
Corba de Peano traçada unint els punts centrals dels successius quadrats en què hom divideix el quadrat inicial
© fototeca.cat
Matemàtiques
Donat un quadrat, corba que, amb una longitud finita des del seu començament, ateny qualsevol punt del quadrat inicialment fixat.
problema de Waring
Matemàtiques
Problema de la teoria de nombres proposat pel matemàtic anglès Edward Waring (Old Heath 1734-98) l’any 1770, consistent a demostrar que per a qualsevol nombre natural n existeix un nombre associat K (n), de manera que qualsevol natural pot ésser representat com una suma, com a màxim, de K (n) termes, cada terme essent una potencia n-èsima d’un natural.
En particular, cada nombre natural hauria de poder ésser representat com a suma de quatre quadrats com a màxim i com a suma de nou cubs Aquest problema fou resolt per Hilbert el 1909
Ferdinand Gotthold Max Eisenstein
Matemàtiques
Matemàtic alemany.
Investigà sobre la teoria dels nombres, les funcions ellíptiques i els determinants Demostrà el teorema general de representació de nombres mitjançant una suma de quadrats i descobrí el criteri d’irreductibilitat que duu el seu nom
filtratge
Matemàtiques
Mètode numèric per a estimar el valor real d’una magnitud a partir del valor d’una mesura seva.
La diferència entre ambdós valors és anomenada soroll i, per hipòtesi, és una variable aleatòria Entre els mètodes de filtratge hom distingeix els lineals mínims quadrats, mitjanes mòbils i allisatge exponencial i els no lineals mètode de Fourier, de la transformació en z i de Kalman Té aplicació en la predicció i en la previsió
ajust
Matemàtiques
Operació estadística que consisteix a trobar la llei que resumeix, de la millor manera possible, la variació d’una variable aleatòria Y
en funció d’una altra variable X
, de la qual depèn.
Hom fa l’ajust a partir del coneixement de parells de valors x,y obtinguts observant una mostra, com la capacitat pulmonar i l’edat Deixant de banda l’ajust purament gràfic allisatge, habitualment hom pren una funció f x lineal, exponencial, polinòmica, etc i se suposa que y=f x +ε, on ε és un residu aleatori o soroll, i els paràmetres que defineixen la funció són determinats pel mètode dels mínims quadrats
paral·lelogram
Matemàtiques
Quadrilàter que té els costats oposats paral·lels i, per tant, iguals.
Les diagonals d’un parallelogram es tallen en llur punt mitjà, anomenat centre del parallelogram Si un parallelogram té els quatre costats iguals, és anomenat rombe Si els quatre costats són perpendiculars, és anomenat rectangle Els parallelograms que són rombes i rectangles alhora són anomenats quadrats , i els que no són ni rombes ni rectangles, romboides L’àrea d’un parallelogram resulta de multiplicar la longitud d’un costat, que hom anomena base , per la distància que el separa del seu parallel, anomenada altura
octàedre truncat
Matemàtiques
Políedre que resulta de truncar un octàedre regular per quadrats en cadascun dels seus vèrtexs.
Té 6 cares quadrades i 8 d’hexagonals