Resultats de la cerca
Es mostren 188 resultats
paràbola
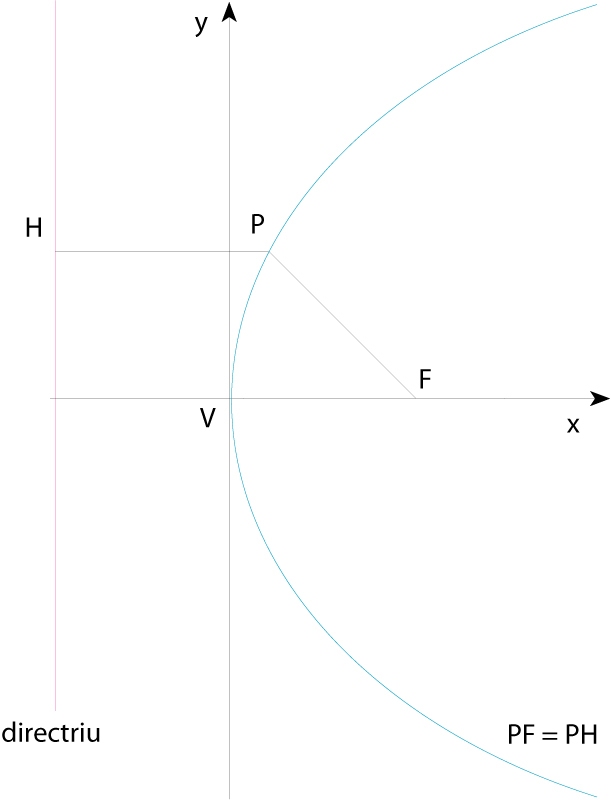
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+ c és una paràbola de vèrtex - b /2 a ,…
operand
Matemàtiques
Qualsevol dels elements que intervenen en una operació per donar el resultat.
Cada operació n'exigeix un nombre fix, normalment dos però també un, o tres, etc segons aquest nombre, l’operació s’anomena diàdica o monàdica com ara la identitat o la complementació, triàdica , etc En algunes operacions els operands reben noms especials segons el lloc que ocupen primer o segon, respectivament augend i addend i sumand qualsevol dels dos en l’addició, minuend i subtrahend en la subtracció, multiplicand i multiplicador i factor qualsevol dels dos en la multiplicació, dividend i divisor en la divisió, implicador o antecedent i implicat o conseqüent en…
variació
Matemàtiques
Qualsevol successió de n elements d’un conjunt de cardinal m, els quals són diferents dos a dos.
El conjunt de totes les possibles variacions de m elements presos de n en n , V n m , té cardinal El quocient de V n m per les possibles permutacions dels n elements P n = n = n n -1 21, dona el nombre de combinacions C n m dels m elements presos de n en n combinació Hom pot repetir cada element un nombre de vegades qualsevol, i això dona lloc a les variacions amb repetició VR n m El nombre d’aquestes és donat per l’expressió VR n m = m n
teorema
Matemàtiques
Qualsevol proposició matemàtica que pot ésser demostrada a partir d’unes hipòtesis, uns axiomes o altres proposicions demostrades anteriorment.
Les proposicions prèvies de demostració breu que precedeixen un teorema de demostració més complicada són dites lemes , mentre que les conseqüències que es deriven del teorema són anomenades corollaris Hom anomena també teorema qualsevol conclusió general que ja ha estat demostrada Una conjectura , en canvi, és una proposició que hom creu certa però en desconeix la demostració Hi ha nombrosos teoremes coneguts, com ara el de Pitàgores, el de Tales, el del valor mitjà, etc Dos teoremes són anomenats recíprocs quan cadascun té per hipòtesi la conclusió de l’altre
focus
Matemàtiques
Punt la distància del qual a qualsevol dels punts d’una corba pot ésser expressada com una funció racional de les coordenades dels punts.
Aquesta definició mètrica de focus, que és una generalització dels focus de les còniques cònica, no permet, però, d’ésser estesa a una corba algèbrica qualsevol, i per aconseguir-ho cal passar a la definició projectiva de focus
angles de direcció
Matemàtiques
Qualsevol dels tres angles positius que té una recta orientada que passa per l’origen respecte dels tres semieixos positius de referència a l’espai.
Els angles de direcció es poden calcular per a qualsevol recta, considerant la parallela corresponent que passa per l’origen En tot cas, cal fixar-ne la direcció
ergodicitat
Matemàtiques
Propietat d’un procés estocàstic en què tots els paràmetres probabilístics es poden determinar (amb probabilitat 1) d’una única funció qualsevol resultant del procés.
Aquesta propietat normalment s’expressa, també, dient que les mitjanes probabilístiques coincideixen amb les temporals En sentit ampli hom parla d’ergodicitat respecte a la mitjana, desviació típica o qualsevol altre paràmetre d’interès Els processos ergòdics són importants en el sentit que hom pot fer fàcilment mesures sobre una única funció resultant d’un fenomen físic, i aplicar els valors resultants a la teoria matemàtica dels processos estocàstics
subgrup
Matemàtiques
Qualsevol subconjunt H d’un grup (G, E) tal, que és estable per a l’operació del grup i té estructura de grup mitjançant aquesta operació induïda.
És un subconjunt no buit tal, que si x, y són d’ell, el resultat x-y també hi pertany El conjunt d’enters amb l’operació addició és un subgrup del grup additiu de nombres racionals Si hom divideix l’ordre de G grup per l’ordre de H, el quocient és anomenat índex de H en G o, simplement, índex de H Segons el teorema de Lagrange, si un grup G té ordre finit i H és qualsevol subgrup de G, l’ordre de G és el producte de l’ordre de H per l’índex de H
espai de Hausdorff
Matemàtiques
Espai topològic X que acompleix l’axioma de Hausdorff (o axioma de separació), segons el qual, per a qualsevol parell de punts distints x, y de X existeix un entorn de x i un altre de y que són disjunts.
És anomenat també espai separat Els espais euclidians de qualsevol dimensió són de Hausdorff
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A -1 La matriu…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina