Resultats de la cerca
Es mostren 30 resultats
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l…
diagrama de Venn
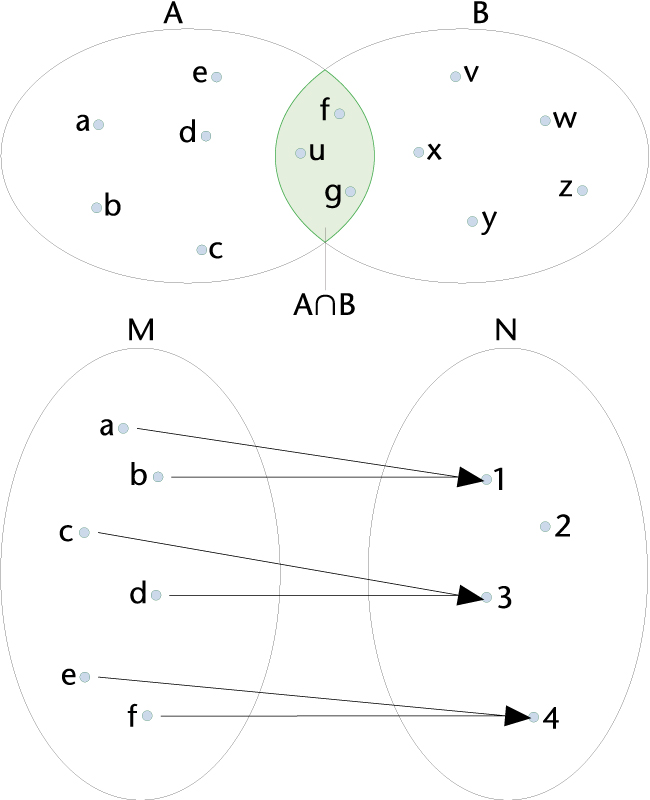
Representació de la intersecció dels conjunts A i B (a dalt) i de l’aplicació del conjunt M en el conjunt N (a baix) per mitjà de diagrames de Venn
© Fototeca.cat
Matemàtiques
Diagrama emprat amb fins didàctics per a representar gràficament conjunts i estudiar les relacions i operacions entre conjunts.
Aquests diagrames foren introduïts pel matemàtic i lògic anglès John Venn 1834-1923 Els conjunts són representats mitjançant cercles o corbes tancades qualssevol Cal no confondre un diagrama de Venn amb la regió del pla limitada pel diagrama És conegut també com a diagrama d’Euler-Venn
Hermann Bondi
Astronomia
Matemàtiques
Matemàtic i cosmòleg anglès d’origen austríac.
Amb Thomas Gold i Fred Hoyle, és l’autor de la teoria cosmològica dita de l’estat estacionari Steady-State de l’univers 1948, que parteix del “principi cosmològic perfecte” segons el qual l’univers presenta el mateix aspecte qualssevol que siguin el lloc i l’instant de l’observació cosmologia La seva obra més important és Cosmologia 1952
postulats d’Euclides
Matemàtiques
Conjunt de cinc principis axiomàtics exposats per Euclides en l’obra Elements, en els quals fonamentà la seva geometria.
Són els següents donats dos punts qualssevol, hom pot traçar una recta que els uneix tota línia recta finita es pot prolongar indefinidament donat un punt qualsevol, hom pot traçar una circumferència amb radi arbitrari i centre en el punt esmentat tots els angles rectes són iguals entre ells i, finalment, donada una recta i un punt exterior, hom només pot traçar per aquest una recta parallela a la recta donada
conjunt ordenat
Matemàtiques
Conjunt X
proveït d’una relació d’ordre ≤.
Si la relació d’ordre és parcial, el conjunt OOO X ,≤OOO és parcialment ordenat i, si és total, és totalment ordenat Una relació d’ordre és parcial si compleix les propietats reflexiva x ≤ x , transitiva si x ≤ y i y ≤ z , aleshores x ≤ z i antisimètrica si x ≤ y i y ≤ x , aleshores x = y I és total quan és parcial i, a més, tota parella d’elements és comparable qualssevol que siguin x , y , x ≤ y o y ≤ x
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
sinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i un segment de longitud unitat OP que forma un angle α amb l’eix d’abscisses x, valor de la projecció de OP sobre l’eix y
.
Aquesta projecció és el sinus de l’angle α i és denotada per sinα El sinus de l’angle α determinat entre dos segments qualssevol és el sinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al sinus d’un angle són sinα+β = sinα cosβ - cosα sinβ sin-α = -sinα sinα sinβ = cosα-β - cosα+β/2 sinα + sinβ = 2 sinα+β/2 cosα-β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α+sin 2 α=1
prisma

Elements d’un prisma (a l’esquerra9 i prisma triangular recte (a la dreta)
© Fototeca.cat
Matemàtiques
Políedre que té dues cares iguals i paral·leles (dites bases), les altres cares (dites cares laterals) essent paral·lelograms.
Les interseccions entre les cares laterals són les arestes laterals Una diagonal és una recta que uneix dos vèrtexs qualssevol, que no són de la mateixa base L' alçada és la distància perpendicular entre les dues bases L' àrea lateral és la suma de les àrees de les cares laterals l' àrea total és l’àrea lateral més l’àrea de les bases, i el volum és el producte de l’àrea d’una base per l’altitud Un prisma és anomenat triangular, quadrangular, pentagonal , etc, si les bases són, respectivament, triangles, quadrilàters, pentàgons, etc Un prisma és anomenat recte si les bases són…
regla dels signes
Matemàtiques
Regla que dona el signe del producte de dos nombres reals qualssevol.
És - a b = - ab = a -b - a - b = a b on a ∈ℝi b ∈ℝ, i pot ésser generalitzada a qualsevol anell commutatiu Hom pot enunciar-la dient que si els signes són iguals el producte és +, i si són diferents és -
relació d’ordre
Matemàtiques
Relació binària R entre els elements d’un conjunt C que és reflexiva, antisimètrica i transitiva.
La parella C, R constitueix un conjunt ordenat És usual la notació ≤per a designar la relació d’ordre desigualtat 5, i a ≤ b és llegit '' a menor o igual a b' , o bé '' a inferior a b' aquesta notació generalitza la coneguda i usual relació “ésser menor que o igual a” que ordena els nombres Unes altres relacions d’ordre importants són la relació d’igualtat, la relació d’inclusió entre conjunts, la relació “ésser divisor de” en els nombres naturals, etc En un conjunt ordenat, són elements notables el màxim , el mínim , el maximal , el minimal , el majorant i el minorant Dos elements…