Resultats de la cerca
Es mostren 159 resultats
distributiu | distributiva
Matemàtiques
Dit d’una llei de composició interna quan satisfà determinades propietats.
En un conjunt E dotat de dues lleis de composició internes o operacions, una d’elles és distributiva respecte a l’altra quan se satisfan les següents propietats si a * b° c = a * b ° a * c hom diu que * és distributiva per l’esquerra respecte a °, si b° c* a = b * a ° c * a llavors, * és distributiva per la dreta respecte a °, i si se satisfan ambdues condicions hom diu que * és distributiva respecte a ° A ℝ, la multiplicació és distributiva respecte a la suma, però no a l’inrevés
límit d’una funció en un punt
Matemàtiques
Valor al qual tendeix la variable dependent de la funció quan la variable independent tendeix al valor del punt en qüestió.
Donada una funció fD ⊂ ℝ → ℝ i un punt del seu domini de definició, a ∈ D , hom diu que el límit de f quan x tendeix a a és λ, o que f tendeix a λ quan x tendeix a a , si per a tot real ε> 0, per petit que sigui, existeix un real δ> 0 tal que si | x-a | 0 tal que si | x - a | A
funció homogràfica
Matemàtiques
Funció f:ℂ→ℂdefinida per f(z)=(az+b)/(cz+d) quan z≠∞ i z≠-d/c, i per f(∞)=a/c i f(-d/c)=∞.
Quan ad - bc ≠0 hom parla de funció homogràfica pròpia , i quan ad - bc =0 de funció homogràfica impròpia
fase
Física
Matemàtiques
Argument de les funcions sinusoïdals (sinus o cosinus), dependents del temps, especialment quan hom les considera en les formes u = U sin (ϖt+ϕ) i u = U cos (ϖt+ϕ).
És emprat per a descriure l’elongació d’un moviment harmònic o el valor d’una magnitud variable en corrent altern Dues magnituds u 1 i u 2 , variables periòdicament amb el mateix període, són en fase quan en tot instant tenen ambdues la mateixa fase altrament presenten una diferència de fase o desfasament , i hom diu que són desfasades Quan són desfasades π radiants hom diu que són en oposició , i quan ho són π/2 radiants, en quadratura El valor de la fase a l’instant t = 0 és anomenat fase inicial
trocoide
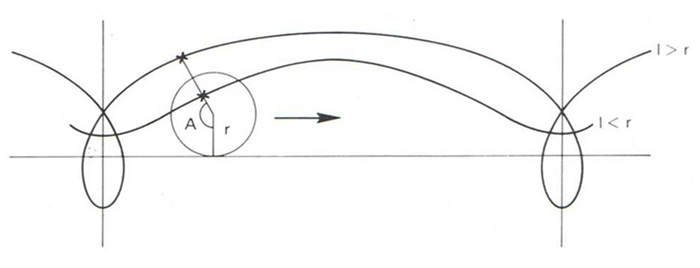
Trociode
© fototeca.cat
Matemàtiques
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
aberrància
Matemàtiques
Singularitat que es presenta quan els valors obtinguts d’un conjunt d’observacions d’una magnitud disten ostensiblement del valor mitjà obtingut amb totes les observacions.
Aquest terme és aplicat quan un nombre reduït de diversos fets presenten d’una manera excepcional unes característiques diferents d’altres fets que, dins el mateix cas, són relativament ben agrupats al voltant d’un valor mitjà
ordre d’infinitud
Matemàtiques
Resultat de comparar dues funcions, f(x) i g(x), que prenen el valor infinit quan x s’acosta a un cert valor a
.
Hom diu que f x i g x són del mateix ordre d’infinitud si el límit del quocient f x / g x , quan x tendeix a a , existeix i és una constant no nulla En el cas que el dit límit sigui zero o bé infinit, hom diu, respectivament, que f x és de menor ordre d’infinitud que g x o bé que f x és de major ordre d’infinitud que g x
successió de Cauchy
Matemàtiques
Successió {Xn} en que la distància entre dos termes, d(xm,xn)>, tendeix a zero quan m,n tendeixen a infinit.
El seu significat és donat un nombre qualsevol ε> 0, existeix un N tal que dx m ,x n > ε quan m,n > N Cal fer notar que tota successió convergent és successió de Cauchy, tenint en compte, tanmateix, que no tota successió de Cauchy és convergent en l’espai mètric de tots els nombres reals, en el qual d α,β = α-β, tota successió de Cauchy és convergent Aquest és un exemple d’un tipus important d’espais mètrics l’espai mètric complet , definit com un espai mètric en el qual tota successió de Cauchy és convergent
exponent
Matemàtiques
Nombre de vegades que es multiplica per ella mateixa la base d’una potència quan l’exponent és un nombre natural: a l’expressió an , an
.
Quan és real, a x , l’exponent és la variable de la funció exponencial
asímptota
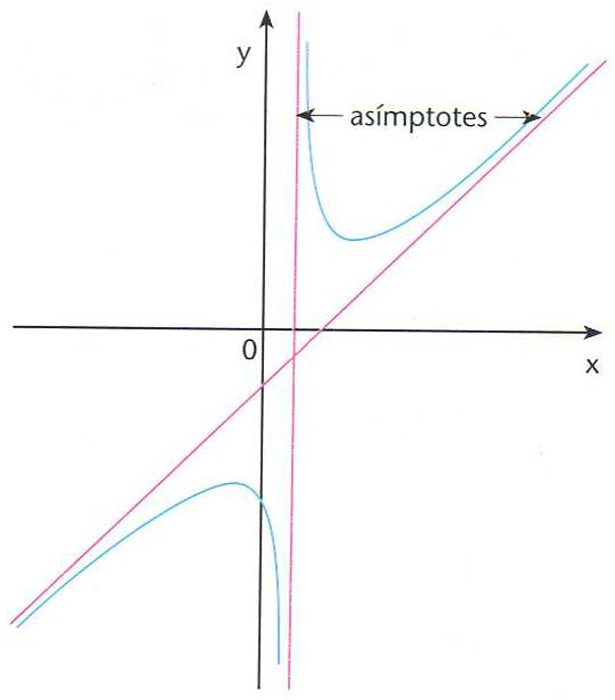
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina