Resultats de la cerca
Es mostren 8 resultats
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament,…
proporció
Matemàtiques
Igualtat de dues raons, fraccions o quocients.
En la proporció a / b = c/d , a i d són dits extrems i b i c , mitjans A partir de la proporció a / b = c/d hom pot derivar altres proporcions a+b / b = c+d / d addició, a + b / a - b = c + d / c-d si a ≠ b addició i subtracció, a/c = b/d alternació, b/a = d/c si a =0 inversió, i a-b / b = c-d / d subtracció
funció trigonomètrica
Matemàtiques
Cadascuna de les funcions que considera la trigonometria, basades en les raons del mateix nom.
cercle goniomètric
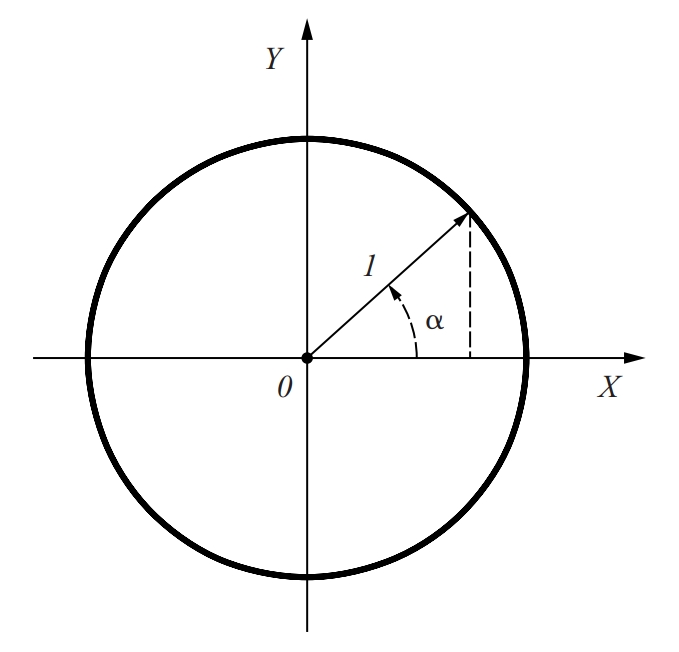
cercle goniomètric
Matemàtiques
Circumferència de radi unitat el centre de la qual és l’origen d’un sistema de coordenades cartesianes (eixos perpendiculars).
És emprat per a definir les raons trigonomètriques d’un angle sinus, cosinus, tangent, etc
teorema de Menelau
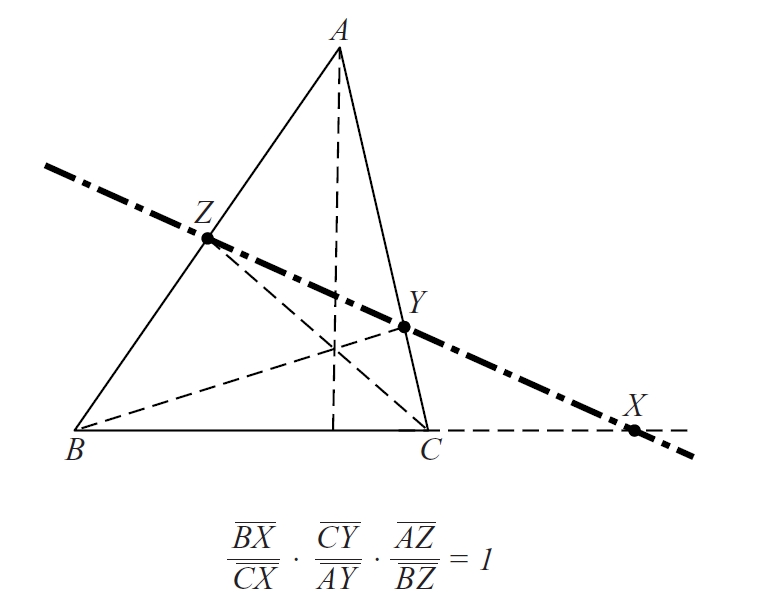
teorema de Menelau
© fototeca.cat
Matemàtiques
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
teorema de Ceva
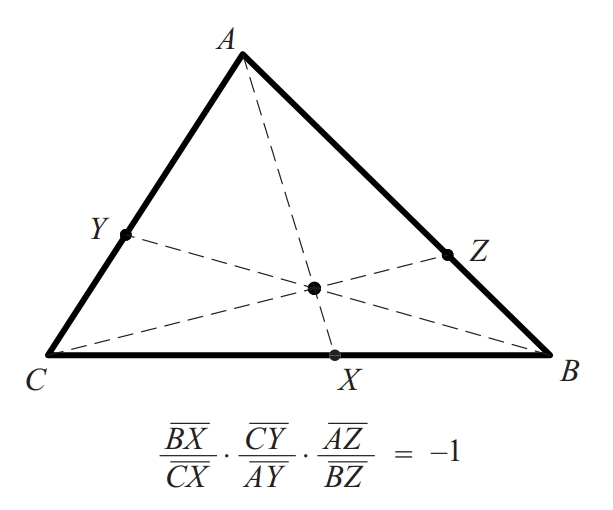
teorema de Ceva
Matemàtiques
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
equiprobable
Matemàtiques
Dit de dos o més esdeveniments que són igualment probables, és a dir, que tenen una llei de probabilitat uniforme.
Aquesta situació es presenta per raons de simetria, com és el cas d’un dau no trucat, i també quan hom obté una mostra representativa d’una població, a base de sortejar els individus que l’han de formar, amb la mateixa probabilitat de figurar-hi, com és el cas d’alguns sondeigs o enquestes
divisió harmònica
Matemàtiques
Conjunt de dues parel·les de punts A,B i C,D d’una mateixa recta tals, que els dos punts d’una mateixa parel·la divideixen el segment format pels dos altres punts en les raons oposades AC/AD = BC/BD.
Cada punt d’aquesta divisió és anomenat conjugat harmònic del seu associat respecte als altres dos