Resultats de la cerca
Es mostren 12 resultats
freqüència
Matemàtiques
En una sèrie de N repeticions d’una experiència en què hom estudia la realització o no realització d’un esdeveniment A, quocient entre el nombre d’esdeveniments en què A es realitza i el nombre total d’esdeveniments, N: f=n/N
.
El nombre f és la freqüència o freqüència relativa de l’esdeveniment A
freqüència
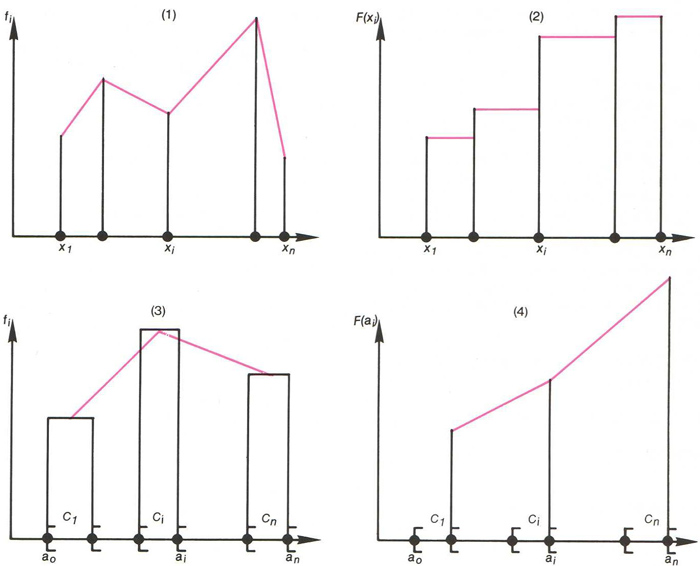
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del…
teorema de Bernoulli
Matemàtiques
Donat un nombre ε arbitràriament petit, la probabilitat que la diferència entre la freqüència relaiva f de l’esdeveniment favorable en una sèrie de proves i la probabilitat p d’aquest esdeveniment sigui, en valor absolut, superior a ε tendeix a zero en augmentar indefinidament el nombre de proves.
O sigui Aquest teorema fa aparèixer el lligam que hi ha entre freqüència relativa i probabilitat, la qual és el valor mitjà de la freqüència per a un nombre molt gran de proves Com que hi intervé un nombre de proves tant gros, aquest teorema és conegut també amb el nom de llei dels grans nombres
asímptota
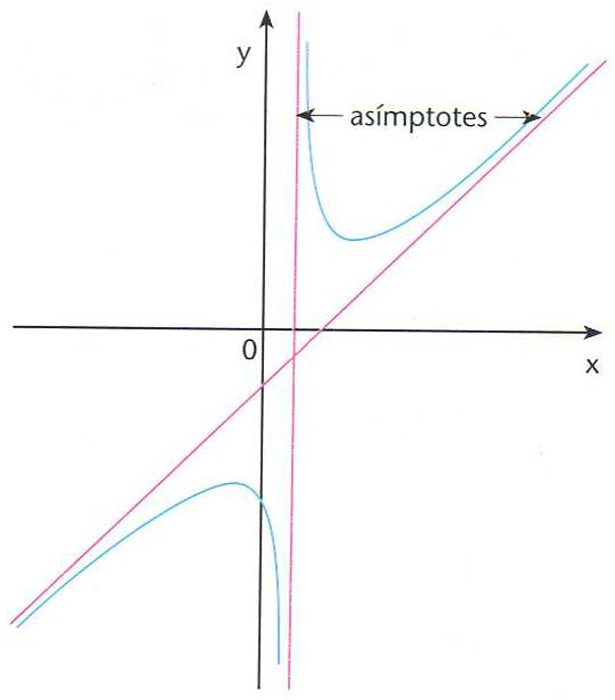
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la hipèrbola té dues…
llei dels grans nombres
Matemàtiques
Teorema intuït per Jakob Bernoulli i P.S.Laplace i batejat així per S.D.Poisson, la demostració del qual, progressivament més i més rigorosa, començà amb P.L.Čebyšev i ha acabat amb E.F.E.Borel, Khinčin, A.N.Kolmogorov, Glivenko i Cantelli.
Una primera formulació de la llei dels grans nombres és la llei feble dels grans nombres , anomenada també teorema de Bernoulli, que estableix que la freqüència relativa d’un esdeveniment al llarg de n temptatives elementals independents convergeix en probabilitat vers la probabilitat de l’esdeveniment Hom diu que una variable aleatòria X n convergeix en probabilitat vers una variable certa A quan la diferència | X n —A | tendeix a 0 en augmentar n , és a dir, quan ε essent tan petit com hom vulgui Una altra formulació de la llei dels grans nombres és l’anomenada llei forta dels…
Jeroni Munyós
Astronomia
Matemàtiques
Judaisme
Hebraista, astrònom i matemàtic.
Hom ha especulat sobre un possible origen judeoconversEs graduà en arts a València, on estudià vers 1530-40 Professor d’hebreu a la Universitat d’Ancona, tornà a València, on fou professor particular de matemàtiques i catedràtic d’hebreu 1563 i de matemàtiques 1567 de la Universitat El 1579 passà a Salamanca com a catedràtic de les mateixes matèries Observà l’anomenat cometa del 1572 , actualment identificat com a Supernova de Tycho Brahe, sobre el qual publicà Libro del Nuevo Cometa el 1573, des d’on atacà la tradicional creença en la immutabilitat dels astres, en determinà la posició …
relació binària
Matemàtiques
Condició relativa a dos elements d’un conjunt que és satisfeta per determinats parells d’elements (eventualment per tots o per cap parell).
Sovint hom representa una relació binària per una taula de doble entrada on són assenyalats els quadres corresponents als parells que satisfan la relació La taula següent dóna la relació a és múltiple de b entre els nombres del conjunt 1,2,3,4,5,6 Entre les relacions binàries sobresurten per llur importància les relacions d’equivalència i les relacions d’ordre
taula de contingència
Matemàtiques
Taula de doble entrada, amb I línies i J columnes, relativa a dos caràcters qualitatius, els quals poden presentar respectivament I i J modalitats.
Siguin n i i n j els efectius totals de la i -èsima fila i de la j -èsima columna, respectivament, i sigui n i j l’efectiu de la casella corresponent, serà l’efectiu o nombre d’individus total observat La serà l’efectiu o nombre d’individus total observat La contingència decada casella és definida com és a dir, la diferència entre l’efectiu observat a la casella i el teòric que li correspondria en la hipòtesi d’independència dels dos caràcters Hom ha definit diferents coeficients que mesuren el grau de dependència entre dos caràcters qualitatius, entre ells els de Pearson i el de Čuprov Hom…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…
hipòtesi estadística
Matemàtiques
Hipòtesi relativa al valor dels paràmetres o a la forma de la llei de probabilitat d’una població, de la qual hom es proposa d’examinar la validesa mitjançant l’observació dels valors d’una variable aleatòria en les mostres tretes d’aquesta població.
La hipòtesi és simple si especifica completament la llei de probabilitat de la variable aleàtoria considerada, i és composta o múltiple en els altres casos